// 无向图的一节点到另一节点的最短路径(边数最少的路径)(采用邻接表存储).cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include<iostream>
#define MAX 100
#define MAXQ 50
using namespace std;
struct edgeNode
{
int no; //边端的序号
char info; //边端的名称
struct edgeNode * next; //下一个
};
struct vexNode
{
char info; //节点名称
struct edgeNode *link; //与之相连的端点
};
//存储节点信息
vexNode adjlist[MAX];
//循环队列
int queue[MAXQ];
//访问标志
bool visited[MAX];
//存储从指定点到每一个点的路径
int parent[MAX];
//建立邻接表存储,返回节点个数
int createGraph(vexNode *adjlist)
{
int n,e;
cout<<"请输入节点数:";
cin>>n;
cout<<"请输入边数:";
cin>>e;
int i;
for(i=1;i<=n;i++)
{
cout<<"请输入节点"<<i<<"的名称:";
cin>>adjlist[i].info;
adjlist[i].link = NULL;
}
edgeNode *p1,*p2;
int v1,v2;
for(i=1;i<=e;i++)
{
cout<<"请输入边"<<i<<"的二端的节点序号:";
cin>>v1>>v2;
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p2 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = v1;
p1->info = adjlist[v1].info;
p1->next = adjlist[v2].link;
adjlist[v2].link = p1;
p2->no = v2;
p2->info = adjlist[v2].info;
p2->next = adjlist[v1].link;
adjlist[v1].link = p2;
}
return n;
}
//广度优先搜索无向无权图,返回起始点
int BFS(vexNode *adjlist,int *queue,bool *visited,int *parent)
{
int front,rear,v1;
cout<<"请输入从哪个序号的点开始搜索:";
cin>>v1;
front = 0;
rear = 1;
queue[rear] = v1;
int i;
//访问标志清空
for(i=1;i<MAX;i++)
visited[i] = false;
visited[v1] = true;
cout<<"广度优先搜索次序为:"<<endl;
cout<<"节点"<<v1<<",名称"<<adjlist[v1].info<<endl;
int vx;
edgeNode *p;
while(front != rear)
{
front = (front + 1)%MAXQ;
vx = queue[front];
p = adjlist[vx].link;
while(p!=NULL)
{
if(!visited[p->no])
{
visited[p->no] = true;
cout<<"节点"<<p->no<<",名称"<<adjlist[p->no].info<<endl;
rear = (rear + 1)%MAXQ;
queue[rear] = p->no;
parent[p->no] = vx;
}
p=p->next;
}
}
return v1;
}
//打印起始点到目标节点的最少边数目的路径(最短路径)
//v是目标节点
void print_line(vexNode *adjlist,int *parent,int v)
{
int j = v;
if(parent[j] != 0)
print_line(adjlist,parent,parent[j]);
cout<<adjlist[j].info<<" ";
}
int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"请输入案例的个数:";
cin>>cases;
while(cases--)
{
//创建邻接表
int n = createGraph(adjlist);
//广度优先搜索
int v1 = BFS(adjlist,queue,visited,parent);
//起始节点没有前驱节点
parent[v1] =0;
int v;
cout<<"请输入目标节点:";
cin>>v;
//打印起始点到目标节点的最少边数目的路径(最短路径)
cout<<"从起始节点"<<adjlist[v1].info<<"到"<<adjlist[v].info<<"节点的最短路径为:"<<endl;
print_line(adjlist,parent,v);
cout<<endl;
}
system("pause");
return 0;
}
------------------------------------------------程序测试------------------------------------------------
请输入案例的个数:1
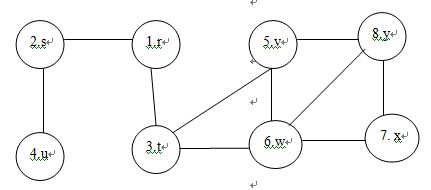
请输入节点数:8
请输入边数:10
请输入节点1的名称:r
请输入节点2的名称:s
请输入节点3的名称:t
请输入节点4的名称:u
请输入节点5的名称:v
请输入节点6的名称:w
请输入节点7的名称:x
请输入节点8的名称:y
请输入边1的二端的节点序号:1 2
请输入边2的二端的节点序号:1 3
请输入边3的二端的节点序号:2 4
请输入边4的二端的节点序号:3 5
请输入边5的二端的节点序号:3 6
请输入边6的二端的节点序号:5 6
请输入边7的二端的节点序号:5 8
请输入边8的二端的节点序号:6 7
请输入边9的二端的节点序号:6 8
请输入边10的二端的节点序号:7 8
请输入从哪个序号的点开始搜索:2
广度优先搜索次序为:
节点2,名称s
节点4,名称u
节点1,名称r
节点3,名称t
节点6,名称w
节点5,名称v
节点8,名称y
节点7,名称x
请输入目标节点:6
从起始节点s到w节点的最短路径为:
s r t w
请按任意键继续. . .
分享到:










相关推荐
在本文中,我们将设计一个算法来求图中一个源点到其他各顶点的最短路径。...本文设计了一种基于邻接表的算法来求图中一个源点到其他各顶点的最短路径,并使用Dijkstra算法和冒泡排序法来实现该算法。
在计算机科学中,无向图的表示方式有很多种,其中邻接表是一种常用的高效存储方法。邻接表相比于邻接矩阵,对于稀疏图(边的数量远小于顶点数量的平方)更为节省空间。 邻接表由一个数组或链表组成,每个元素对应图...
无向图的K最短路径问题是一个在图论和计算机科学中常见的算法问题,它涉及到在无向图中寻找从一个源节点到目标节点的K条最短路径。这个问题在物流规划、网络优化、交通路线设计等多个领域都有广泛应用。下面我们将...
邻接表图是一种非线性数据结构,用于表示有向或无向图。它由一个数组和一组链表组成,数组中的每个元素代表图中的一个顶点,而链表则存储与该顶点相邻的所有顶点。相比于邻接矩阵,邻接表在空间效率上具有优势,因为...
给定一个无向图G,其存储结构为邻接表,我们需要找到从顶点vi到顶点vj的最短路径。这里假设图中各边的权值都相等。 ```plaintext int shortestPath(ALGraph* G, int i, int j) { // 初始化距离数组 int dist...
开发者可能定义了数据结构来表示无向图,如邻接矩阵或邻接表,然后实现了相应的最短路径算法。代码可能还包括了输入/输出功能,以便读取图的结构和打印出最短路径结果。 为了更好地理解并利用这个项目,你需要熟悉...
本代码包着重于解决如何找到无向图中任意两点之间的最短路径,以及所有节点到其他节点的最短路径。以下是对这个主题的详细阐述: 1. **Dijkstra算法**:Dijkstra算法是最常用的一种求解单源最短路径的方法,由荷兰...
最短路径问题可以被定义为:在带权无向图或有向图中寻找两个特定节点间路径的最小代价。在这个硅谷城镇地图问题中,我们可以假设图是有向的,因为通常交通网络都是单向的。权值可能代表距离、行驶时间或者其它相关的...
- **定义**:给定一个无向图G = (V, E),一条从顶点u到顶点v的简单路径是指一系列顶点u, v1, v2, ..., v, 其中(u, v1), (v1, v2), ..., (v-1, v)都是图中的边,并且这些顶点互不相同。 - **应用场景**:在很多实际...
它适用于有向图或无向图,但不适用于负权边,因为其无法保证找到正确的最短路径。 2. Bellman-Ford算法:Bellman-Ford算法可以处理包含负权重边的图,通过松弛操作逐步更新所有节点到源节点的最短路径。它执行V-1次...
- **Dijkstra算法** 是寻找有向图中单源最短路径的常用算法。它通过维护一个优先队列来逐步扩展当前已知最短路径的顶点集合,直到找到目标顶点。 - **Floyd-Warshall算法** 用于找出所有顶点对之间最短路径,通过...
最后,**最小生成树** 是图论中的一个重要概念,它在加权无向图中寻找一棵包括所有顶点的树,使得树的所有边的权重之和最小。经典的算法有: 1. **Prim算法** 从任意一个顶点开始,每次添加一条与已选顶点集合形成...
2. **Floyd-Warshall算法**:这是一个解决所有对最短路径问题的动态规划方法,适合处理带权的有向图或无向图。Floyd-Warshall算法通过逐步更新所有节点对之间的最短路径,最终得到完整的最短路径矩阵。C#实现时,...
对于无向图,邻接矩阵是对称的,因为每条边连接两个顶点,所以在矩阵中这两点的对应元素都是相同的。而对于有向图,邻接矩阵可能不对称,因为边的方向性决定了从一个顶点到另一个顶点可能存在边,反之则不一定。 在...
《数据结构课程设计》最短路径问题实验报告主要围绕如何设计和实现一个交通咨询系统,该系统能够解决从一个城市到另一个城市的最短路径、最低花费或最少时间的问题。在这个实验报告中,我们重点关注以下几个核心知识...
由荷兰计算机科学家艾兹格·迪科斯彻于1956年提出,这个算法广泛应用于网络路由、地理信息系统以及各种有向或无向图的最短路径计算。 ### 算法概述 Dijkstra算法的核心思想是使用贪心策略,每次选取当前未访问节点...
该算法主要用于寻找带权重的有向或无向图中,从一个特定顶点到其他所有顶点的最短路径。Dijkstra算法的核心思想是贪心策略,它每次选择当前未访问顶点中距离起点最近的一个,并更新与它相邻的顶点的距离。 源代码...
邻接表是一种节省空间的图存储方式,特别适合于稀疏图(边的数量远小于节点数量的平方)。对于每个节点,邻接表维护了一个列表,包含所有与该节点相连的节点。这种结构的优点在于,不相关的节点之间不需要额外的空间...
它能够找到一个加权有向或无向图中,从源节点到其他所有节点的最短路径。这个算法的关键在于维护一个优先队列,用于存储待处理的节点,并逐步更新每个节点的最短路径。 以下是Dijkstra算法的基本步骤: 1. 初始化...
图可以分为有向图(edges有方向)和无向图(edges无方向),根据实际情况选择合适的类型。 为了在C++中表示图,我们通常使用邻接矩阵或邻接表。邻接矩阵是一个二维数组,其中的元素表示顶点对之间是否存在边以及边...