求有向图的强连通分支（邻接表存储）C++实现

// 强连通分支（邻接表存储）.cpp : Defines the entry point for the console application.
//通过二次利用深度优先搜索访问节点，每次的深度优先搜索操作不同

#include "stdafx.h"
#include<iostream>
#define MAX 100
using namespace std;

//深度搜索访问节点层次标志枚举变量
enum Color{white,gray,black};

//边端点结构体
struct edgeNode
{
int no; //边尾端的序号
char info; //边端的名称
struct edgeNode * next; //下一个
};

//节点结构体
struct vexNode
{
char info; //节点名称
struct edgeNode *link; //与之相连的端点
};

//强连通子图的链表头结构体
struct StronConHead
{
int num; // 强连通子图序号
struct StronConNode *link; //此强连通子图的第一个节点
};

//
struct StronConNode
{
int num; //一个强连通子图节点的序号
char info; //一个强连通子图节点的名称
struct StronConNode *next; //下一个
};

//深度搜索访问节点的开始/完成时间结构体
struct Time
{
int num; //节点序号
int time; //时间
};

//存储节点信息,adjlist1存储图，adjlist2存储图的转置
vexNode adjlist1[MAX],adjlist2[MAX];
//访问层次
//还没访问为white，访问了但是还没完成它的所有后裔的搜索为gray
//完成它的所有后裔的搜索为black
Color color[MAX];
//访问的开始时间
Time d[MAX];
//访问的完成时间
Time f[MAX];
//深度搜索时，访问过的节点标志
bool visited[MAX];
//con[j]是序号为j的强连通子图的链表头数组，
StronConHead con[MAX];

//建立邻接表存储与其转置
//adjlist1为节点集，adjlist2为图转置节点集，n为节点个数，e为边数目
void createGraph(vexNode *adjlist1,vexNode *adjlist2,int n,int e)
{
int i;
for(i=1;i<=n;i++)
{
cout<<"请输入节点"<<i<<"的名称：";
cin>>adjlist1[i].info;
adjlist2[i].info = adjlist1[i].info;
adjlist1[i].link = NULL;
adjlist2[i].link = NULL;
}
edgeNode *p1,*p2;
int v1,v2;
for(i=1;i<=e;i++)
{
cout<<"请输入边"<<i<<"的起始节点序号：";
cin>>v1;
cout<<"请输入边"<<i<<"的尾节点序号：";
cin>>v2;
//建立原图邻接表
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = v2;
p1->info = adjlist1[v2].info;
p1->next = adjlist1[v1].link;
adjlist1[v1].link = p1;
//建立转置图邻接表
p2 = (edgeNode*)malloc(sizeof(edgeNode));
p2->no = v1;
p2->info = adjlist2[v1].info;
p2->next = adjlist2[v2].link;
adjlist2[v2].link = p2;
}
}

//深度优先搜索有向无权图
//adjlist1为原图的邻接表存储，time为一个全局时间戳，v是第几个节点
void DFS1(vexNode *adjlist1,int &time,int v)
{
color[v] = gray;
time += 1;
d[v].num = v;
d[v].time = time;
edgeNode *p;
p = adjlist1[v].link;
while(p != NULL)
{
if(color[p->no]==white)
{
DFS1(adjlist1,time,p->no);
}
p = p->next;
}
color[v] = black;
time += 1;
f[v].num = v;
f[v].time = time;
}

////降序排列第一次深度搜索各节点的完成时间
void fast_sort_f(Time *f,int begin,int end)
{
if(begin<end)
{
int i = begin-1, j = begin;
f[0] = f[end];
while(j<end)
{
if(f[j].time>f[0].time)
{
i++;
Time temp = f[i];
f[i] = f[j];
f[j] = temp;
}
j++;
}
Time temp1 = f[end];
f[end] = f[i+1];
f[i+1] = temp1;
fast_sort_f(f,begin,i);
fast_sort_f(f,i+2,end);
}
}
//深度优先搜索有向无权图的转置图
//adjlist2为转置图的邻接表存储，con是序号为no的强连通子图的链表头数组，
//time为一个全局时间戳，v是第几个节点
void DFS2(vexNode *adjlist2,StronConHead *con,int &no,int v)
{
visited[v] = true;
StronConNode *p1 = (StronConNode*)malloc(sizeof(StronConHead));
p1->info = adjlist2[v].info;
p1->num = v;
p1->next = con[no].link;
con[no].link = p1;
edgeNode *q1;
q1 = adjlist2[v].link;
while(q1 != NULL)
{
if(!visited[q1->no])
{
DFS2(adjlist2,con,no,q1->no);
}
q1 = q1->next;
}
}

////打印各个强连通分支节点
//con是序号为no的强连通子图的链表头数组，no是强连通全局分支序号
void print_StronConCom(StronConHead *con,int &no)
{
int i;
StronConNode * p;
for(i=1;i<no;i++)
{
cout<<"强连通分支"<<i<<"：";
p = con[i].link;
while(p !=NULL)
{
cout<<"("<<p->num<<":"<<p->info<<") ";
p = p->next;
}
cout<<endl;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"请输入案例的个数：";
cin>>cases;
while(cases--)
{
int n,e;
cout<<"请输入节点数：";
cin>>n;
cout<<"请输入边数：";
cin>>e;
//访问节点的时间戳，全局变量
int time = 0;
//no是强连通全局分支序号，全局变量
int no = 1;
//访问标志清空与前驱节点都初始化为0
int i;
for(i=1;i<=n;i++)
{
color[i] = white;
visited[i] = false;
con[i].link = NULL;
}
//创建邻接表
createGraph(adjlist1,adjlist2,n,e);
//第一次深度搜索，搜索原图
for(i=1;i<=n;i++)
{
if(color[i]==white)
DFS1(adjlist1,time,i);
}
//降序排列第一次深度搜索各节点的完成时间
fast_sort_f(f,1,n);
//第二次深度搜索，搜索原图的转置图
for(i=1;i<=n;i++)
{
if(!visited[i])
{
DFS2(adjlist2,con,no,f[i].num);
no += 1;
}
}
//打印各个强连通分支节点
print_StronConCom(con,no);
}
system("pause");
return 0;
}

--------------------------------------------------程序测试-----------------------------------------------------

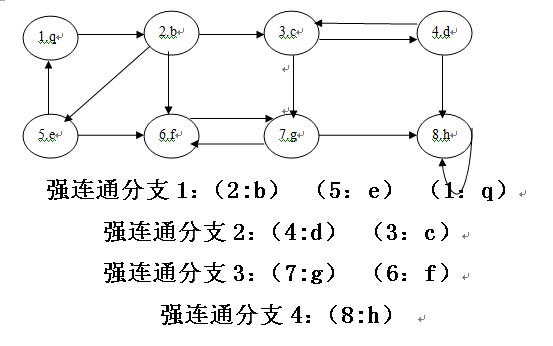
请输入案例的个数：1
请输入节点数：8
请输入边数：14
请输入节点1的名称：q
请输入节点2的名称：b
请输入节点3的名称：c
请输入节点4的名称：d
请输入节点5的名称：e
请输入节点6的名称：f
请输入节点7的名称：g
请输入节点8的名称：h
请输入边1的起始节点序号：1
请输入边1的尾节点序号：2
请输入边2的起始节点序号：2
请输入边2的尾节点序号：3
请输入边3的起始节点序号：2
请输入边3的尾节点序号：6
请输入边4的起始节点序号：2
请输入边4的尾节点序号：5
请输入边5的起始节点序号：3
请输入边5的尾节点序号：4
请输入边6的起始节点序号：3
请输入边6的尾节点序号：7
请输入边7的起始节点序号：4
请输入边7的尾节点序号：3
请输入边8的起始节点序号：4
请输入边8的尾节点序号：8
请输入边9的起始节点序号：5
请输入边9的尾节点序号：1
请输入边10的起始节点序号：5
请输入边10的尾节点序号：6
请输入边11的起始节点序号：6
请输入边11的尾节点序号：7
请输入边12的起始节点序号：7
请输入边12的尾节点序号：6
请输入边13的起始节点序号：7
请输入边13的尾节点序号：8
请输入边14的起始节点序号：8
请输入边14的尾节点序号：8
强连通分支1：(2:b) (5:e) (1:q)
强连通分支2：(4:d) (3:c)
强连通分支3：(7:g) (6:f)
强连通分支4：(8:h)
请按任意键继续. . .