最小生成树Prim算法实现（采用邻接表存储）C++实现

// Prim算法实现（采用邻接表存储）.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include "stdafx.h"
#include<iostream>
#define MAX 100
#define Infinity 65535
typedef int WeiType;
using namespace std;

struct edgeNode
{
int no; //边端的序号
char info; //边端的名称
WeiType weight; //边的权值
struct edgeNode * next; //下一个
};

struct vexNode
{
char info; //节点名称
struct edgeNode *link; //与之相连的端点
};

//存储节点信息
vexNode adjlist[MAX];
//访问标志
bool visited[MAX];
//lowcost[j]存储从开始节点到节点j的最小花费
WeiType lowcost[MAX];
//parent[j]表示节点j的前驱节点
int parent[MAX];

//建立邻接表存储
void createGraph(vexNode *adjlist,const int n,const int e,const int v0)
{

int i;
for(i=1;i<=n;i++)
{
cout<<"请输入节点"<<i<<"的名称：";
cin>>adjlist[i].info;
adjlist[i].link = NULL;
//初始化
visited[i] = false;
lowcost[i] = Infinity;
parent[i] = v0;
}
edgeNode *p1,*p2;
int v1,v2;
WeiType weight;
for(i=1;i<=e;i++)
{
cout<<"请输入边"<<i<<"的二端的节点序号：";
cin>>v1>>v2;
cout<<"此边的权值：";
cin>>weight;
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p2 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = v1;
p1->weight = weight;
p1->info = adjlist[v1].info;
p1->next = adjlist[v2].link;
adjlist[v2].link = p1;
p2->no = v2;
p2->weight = weight;
p2->info = adjlist[v2].info;
p2->next = adjlist[v1].link;
adjlist[v1].link = p2;
}
}

int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"请输入案例的个数：";
cin>>cases;
while(cases--)
{
int n,e;
cout<<"请输入节点数：";
cin>>n;
cout<<"请输入边数：";
cin>>e;
cout<<"请输入从哪一个节点开始：";
int v;
cin>>v;
int i,j;
//最小生成树的权值总和
WeiType sum = 0;
createGraph(adjlist,n,e,v);
edgeNode *p,*q;
p = adjlist[v].link;
visited[v] = true;
while(p!=NULL)
{
lowcost[p->no] = p->weight;
p = p->next;
}
WeiType minCost;
for(i=1;i<n;i++)
{
minCost = Infinity;
int k;
for(j=1;j<=n;j++)
{
if(minCost>lowcost[j]&&!visited[j])
{
minCost = lowcost[j];
k = j;
}
}
sum += minCost;
visited[k] = true;
q = adjlist[k].link;
while(q != NULL)
{
if(!visited[q->no]&&q->weight<lowcost[q->no])
{
lowcost[q->no] = q->weight;
parent[q->no] = k;
}
q = q->next;
}
}
cout<<"最小生成树的边集为："<<endl;
for(i=1;i<=n;i++)
if(i!=v)
cout<<"("<<adjlist[parent[i]].info<<","<<adjlist[i].info<<")"<<" ";
cout<<endl;
cout<<"最小生成树的权值为："<<sum<<endl;
}
system("pause");
return 0;
}

-----------------------------------------------------程序测试--------------------------------------------------

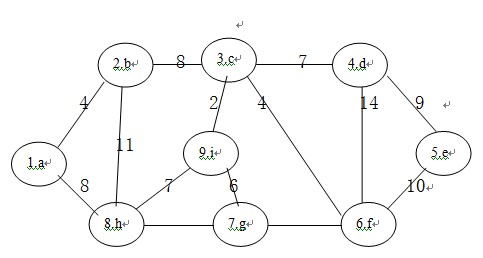
请输入案例的个数：1
请输入节点数：9
请输入边数：14
请输入从哪一个节点开始：2
请输入节点1的名称：a
请输入节点2的名称：b
请输入节点3的名称：c
请输入节点4的名称：d
请输入节点5的名称：e
请输入节点6的名称：f
请输入节点7的名称：g
请输入节点8的名称：h
请输入节点9的名称：i
请输入边1的二端的节点序号：1 2
此边的权值：4
请输入边2的二端的节点序号：1 8
此边的权值：8
请输入边3的二端的节点序号：2 3
此边的权值：8
请输入边4的二端的节点序号：2 8
此边的权值：11
请输入边5的二端的节点序号：3 4
此边的权值：7
请输入边6的二端的节点序号：3 6
此边的权值：4
请输入边7的二端的节点序号：3 9
此边的权值：2
请输入边8的二端的节点序号：4 5
此边的权值：9
请输入边9的二端的节点序号：4 6
此边的权值：14
请输入边10的二端的节点序号：5 6
此边的权值：10
请输入边11的二端的节点序号：6 7
此边的权值：2
请输入边12的二端的节点序号：7 8
此边的权值：1
请输入边13的二端的节点序号：7 9
此边的权值：6
请输入边14的二端的节点序号：8 9
此边的权值：7
最小生成树的边集为：
(b,a) (b,c) (c,d) (d,e) (c,f) (f,g) (g,h) (c,i)
最小生成树的权值为：37
请按任意键继续. . .