// 单源最短路径Dijkstra算法实现.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include<iostream>
#define MAX 200
#define Infinity 65535
using namespace std;
//边尾节点信息结构体
struct edgeNode
{
int no; //尾接点序号
int cost; //边权值
edgeNode *next; //其下一条邻接边尾节点指针
};
//节点信息结构体
struct vexNode
{
char info; //节点名称
edgeNode *link; //与其相连的边的尾节点链表指针
};
struct Queue
{
int no; //队列中节点序号
int cost; //以此为尾节点的边的权值
};
//优先队列
Queue priQue[MAX];
//节点数组
vexNode adjlist[MAX];
//指定源点到节点i的最短路径花费
int lowcost[MAX];
//指定源点到节点i路径中,节点i的前驱节点序号
int parent[MAX];
//建立图邻接表
void createGraph(vexNode *adjlist,int *parent,int * lowcost,const int n,const int e)
{
int i;
for(i=1;i<=n;i++)
{
cout<<"请输入节点"<<i<<"的名称:";
cin>>adjlist[i].info;
adjlist[i].link = NULL;
lowcost[i] = Infinity;
parent[i] = i;
}
edgeNode *p1;
int v1,v2;
for(i=1;i<=e;i++)
{
cout<<"请输入边"<<i<<"的起始节点与尾节点序号:";
cin>>v1>>v2;
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = v2;
cout<<"此边的权值:";
cin>>p1->cost;
p1->next = adjlist[v1].link;
adjlist[v1].link = p1;
}
}
//当插入节点到优先队列时,保持队列优先性
void keep_min_heap(Queue *priQue,int &num,const int k)
{
int l = 2*k;
int r = 2*k + 1;
int smallest = k;
if(l<=num&&priQue[l].cost<priQue[k].cost)
smallest = l;
if(r<=num&&priQue[r].cost<priQue[smallest].cost)
smallest = r;
if(smallest != k)
{
Queue temp = priQue[smallest];
priQue[smallest] = priQue[k];
priQue[k] = temp;
keep_min_heap(priQue,num,smallest);
}
}
//插入节点到优先队列时并且保持队列优先性
void heap_insert(Queue *priQue,int &num,int no,int cost)
{
num +=1;
priQue[num].no = no;
priQue[num].cost = cost;
int i = num;
while(i>1&&priQue[i/2].cost>priQue[i].cost)
{
Queue temp = priQue[i];
priQue[i] = priQue[i/2];
priQue[i/2] = temp;
i = i/2;
}
}
//取出优先队列的队头元素
Queue heap_extract_min(Queue *priQue,int &num)
{
if(num<1)
return priQue[0];
Queue min = priQue[1];
priQue[1] = priQue[num];
num -=1;
keep_min_heap(priQue,num,1);
return min;
}
//打印指定源点带序号为i的点的最短路径
void print_it(int *parent,vexNode *adjlist,int v)
{
if(parent[v] == v)
cout<<"("<<v<<":"<<adjlist[v].info<<") ";
else
{
print_it(parent,adjlist,parent[v]);
cout<<"("<<v<<":"<<adjlist[v].info<<") ";
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"请输入案例的个数:";
cin>>cases;
while(cases--)
{
int n,e;
cout<<"请输入节点数:";
cin>>n;
cout<<"请输入边数:";
cin>>e;
//队列中的元素,初始为0
int num = 0;
int i;
//创建邻接表
createGraph(adjlist,parent,lowcost,n,e);
cout<<endl;
cout<<"从哪个节点开始:";
int v0;
cin>>v0;
int v =v0;
lowcost[v0] = 0;
cout<<endl;
Queue queue;
for(i=1;i<n;i++)
{
edgeNode *p = adjlist[v0].link;
while(p != NULL)
{
if(lowcost[v0] + p->cost<lowcost[p->no])
{
lowcost[p->no] = lowcost[v0] + p->cost;
parent[p->no] = v0;
heap_insert(priQue,num,p->no,lowcost[p->no]);
}
p = p->next;
}
queue = heap_extract_min(priQue,num);
v0 = queue.no;
}
for(i=1;i<=n;i++)
{
mincost = 0;
cout<<"从点"<<adjlist[v].info<<"开始到"<<adjlist[i].info<<"的最短路径为:"<<endl;
print_it(parent,adjlist,i);
cout<<endl;
cout<<"距离为:"<<lowcost[i]<<endl;
}
}
system("pause");
return 0;
}
--------------------------------------------------程序测试-----------------------------------------------------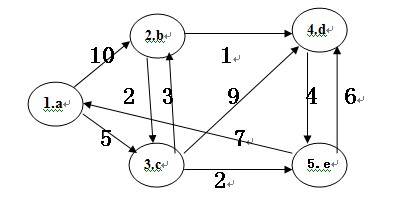
请输入案例的个数:1
请输入节点数:5
请输入边数:10
请输入节点1的名称:a
请输入节点2的名称:b
请输入节点3的名称:c
请输入节点4的名称:d
请输入节点5的名称:e
请输入边1的起始节点与尾节点序号:1 2
此边的权值:10
请输入边2的起始节点与尾节点序号:1 4
此边的权值:5
请输入边3的起始节点与尾节点序号:2 3
此边的权值:1
请输入边4的起始节点与尾节点序号:2 4
此边的权值:2
请输入边5的起始节点与尾节点序号:3 5
此边的权值:4
请输入边6的起始节点与尾节点序号:4 2
此边的权值:3
请输入边7的起始节点与尾节点序号:4 3
此边的权值:9
请输入边8的起始节点与尾节点序号:4 5
此边的权值:2
请输入边9的起始节点与尾节点序号:5 1
此边的权值:7
请输入边10的起始节点与尾节点序号:5 3
此边的权值:6
从哪个节点开始:1
从点a开始到a的最短路径为:
(1:a)
距离为:0
从点a开始到b的最短路径为:
(1:a) (4:d) (2:b)
距离为:8
从点a开始到c的最短路径为:
(1:a) (4:d) (2:b) (3:c)
距离为:9
从点a开始到d的最短路径为:
(1:a) (4:d)
距离为:5
从点a开始到e的最短路径为:
(1:a) (4:d) (5:e)
距离为:7
请按任意键继续. . .
分享到:










相关推荐
本设计以VC++6.0作为程序开发环境,C语言作为程序开发语言,详细介绍了最短路径的求解算法及其...请用C/C++语言的结构体、指针、数据结构等基础知识,编写程序实现图的结构定义、图的存储,以及求解单源点最短路径。
用C++实现的贪心算法 Dijkstra 单源最短路径,并包含大量的注释,对理解程序很有帮助
本篇文章将深入探讨单源最短路径算法,并通过VC++环境下的C++代码实现来帮助理解。 首先,我们要了解几种常见的单源最短路径算法: 1. **Dijkstra算法**:由荷兰计算机科学家艾兹格·迪科斯彻于1956年提出,适用于...
图论算法库 C++ 语言实现 代码内容 图论算法库,包括以下算法: 单源最短路径 Dijkstra 算法 单源最短路径 Bellman-Ford 算法 最小生成树 Prim 算法 每对节点间最短路径 Flod-Warshall 算法
DIJKSTRA单源最短路径算法C/C++实现,内有注释,输入邻接矩阵,输入源点到终点最短路径长度。
总的来说,这个源代码提供了贪心算法解决单源最短路径问题的一个实例,对于理解Dijkstra算法及其在C++中的实现具有参考价值。通过分析和运行这段代码,学习者可以深入理解贪心算法的运作机制,并进一步掌握图论和...
1. **Dijkstra算法**:由Edsger Dijkstra于1956年提出,是最常用的解决单源最短路径的方法。该算法基于贪心策略,每次选取当前未访问节点中与源节点距离最短的一个,并更新其相邻节点的距离。Dijkstra算法适用于非负...
解决单源点最短路径问题的方法有很多,例如Dijkstra算法和Floyd-Warshall算法。Dijkstra算法是一种贪心算法,它通过每次选择当前未访问顶点中距离源点最近的一个来逐步构建最短路径。 **Dijkstra算法的基本步骤**:...
"delta-stepping"算法是求解SSSP的一种高效方法,它基于Dijkstra算法的思想,但通过分层更新节点的最短路径来提高效率。算法的核心在于,它不是每次处理一个节点,而是每次处理一批距离源点s特定步长的节点。具体...
"Dijkstra算法最短路径的C++实现与输出路径" Dijkstra算法是解决单源最短路径问题的经典算法, 由荷兰计算机科学家Edsger W. Dijkstra在1956年提出。该算法可以解决从某个源点到其他所有顶点的最短路径问题。 ...
综上所述,Dijkstra算法和Floyd-Warshall算法是图论中最短路径问题的重要工具,掌握它们的原理和C++实现,不仅可以提升编程技能,还能在实际问题中找到最优解。通过不断实践和深入理解,你可以更好地运用这些算法...
Dijkstra算法适用于单源最短路径问题,而Floyd-Warshall则可以处理所有对之间最短路径的问题。 1. **Dijkstra算法**: Dijkstra算法是一种贪心算法,它从源节点开始,逐步扩展最短路径树,直到到达目标节点。每个...
### 单源最短路径算法实现 #### 一、引言 在计算机科学与图论领域,单源最短路径问题是指在一个加权图中找到从一个特定顶点(源点)到所有其他顶点的最短路径的问题。这类问题在实际应用中非常常见,例如在地图导航...
在压缩包中提供的"最短路径Dijkstra算法"可能包含了C++源代码文件,这些文件可能包含类定义、函数实现以及测试用例,用于演示如何在实际项目中应用Dijkstra算法。通过阅读和理解这些代码,你可以深入学习和掌握...
Dijkstra算法是由荷兰计算机科学家艾兹格·迪科斯彻在1956年提出的,主要用于解决单源最短路径问题。它保证找到的路径是最优的,即每次扩展的边都是当前未访问节点中最短的。Dijkstra算法的基本思想是使用优先队列...
在本项目中,开发者在Visual Studio 2008(VS2008)环境下使用C++语言实现了Dijkstra算法,以解决有向图中的最短路径问题。 首先,我们需要理解Dijkstra算法的基本原理。它通过贪心策略,每次选取当前未访问节点中...
综上所述,Dijkstra算法是解决单源最短路径问题的重要工具,尤其适用于C++这样的编程语言。在这个实例中,通过分析城市地图和应用Dijkstra算法,我们可以找到建立医院的最佳位置,以最大程度地满足所有居民的便利性...
在"单源最短路径"这个压缩包中,很可能包含了以上一种或多种算法的C++实现。源代码可能会包含以下几个部分: - 定义图的结构:通常用邻接矩阵或邻接表来表示图。 - 初始化最短路径:通常将源节点的路径长度设为0,...
在图论中,迪杰斯特拉算法是一种常用的寻找单源最短路径问题的算法。该算法由荷兰计算机科学家艾兹赫·迪杰斯特拉(Edsger W. Dijkstra)于1959年提出。 迪杰斯特拉算法的基本思想 迪杰斯特拉算法的基本思想是依照...