- жµПиІИ: 449512 жђ°
- жАІеИЂ:

- жЭ•иЗ™: иЛПеЈЮ
-

жЦЗзЂ†еИЖз±ї
- еЕ®йГ®еНЪеЃҐ (355)
- Java (180)
- Jquery (18)
- Js (27)
- Mysql (3)
- Windows (6)
- C++ (1)
- Css (9)
- English (35)
- Sqlserver (1)
- Database (3)
- Git (1)
- Linux (5)
- Solr (1)
- Fun (5)
- C (2)
- Test (1)
- Math (2)
- Nlp (8)
- Algorithm (7)
- Regex (9)
- Other (5)
- Html (8)
- ASP (4)
- Access (2)
- Servlet (1)
- Lucene (3)
- Uml (2)
- Struts (19)
- Hibernate (5)
- Jstl (1)
- El (1)
- Python (1)
- SSH (2)
- Spring (1)
- Tomcat (4)
- Jsp (2)
- SE (1)
- Android (2)
- Excel (1)
- Ehcache (1)
- Flash (1)
- Pattern (1)
- Hadoop (1)
з§ЊеМЇзЙИеЭЧ
- жИСзЪДиµДиЃѓ ( 0)
- жИСзЪДиЃЇеЭЫ ( 0)
- жИСзЪДйЧЃз≠Ф ( 0)
е≠Шж°£еИЖз±ї
- 2013-10 ( 1)
- 2013-09 ( 10)
- 2013-08 ( 4)
- жЫіе§Ъе≠Шж°£...
жЬАжЦ∞иѓДиЃЇ
-
huguyue1988пЉЪ
жАОдєИж†ЈеПѓдї•еИ§жЦ≠иЃњйЧЃзЪДйЯ≥дєРеК†иљљеЃМжИРдЇЖеСҐпЉЯжИСзЪДзХМйЭҐи¶БеК†иљље§ЪдЄ™ињЩдЄ™зЪД ...
jPlayerзЪДдЄАдЇЫзФ®ж≥Х -
ж∞ЄдЄНжВФдљ†пЉЪ
[color=yellow][/c[*][img][/img] ...
MyEclipse 9.0ињРи°МйАЯеЇ¶дЉШеМЦ -
tianyalinfengпЉЪ
ињЩдЄ™жХЩз®ЛйЗМйГљжЬЙеРІ
jquery з≠ЫйАЙеЩ® -
mengfei86пЉЪ
䚆姙зЙЫдЇЖпЉМжИСжЙЊдЇЖеНК姩зЪДйЧЃйҐШпЉМдљ†дЄАеП•дї£з†БжРЮеЃЪдЇЖпЉМи∞ҐдЇЖпЉМid^, ...
jquery з≠ЫйАЙеЩ®
lTrieеОЯзРЖ
TrieзЪДж†ЄењГжАЭжГ≥жШѓз©ЇйЧіжНҐжЧґйЧігАВеИ©зФ®е≠Чзђ¶дЄ≤зЪДеЕђеЕ±еЙНзЉАжЭ•йЩНдљОжߕ胥жЧґйЧізЪДеЉАйФАдї•иЊЊеИ∞жПРйЂШжХИзОЗзЪДзЫЃзЪДгАВ
 
lTrieжАІиі®
е•ље§ЪдЇЇиѓіtrieзЪДж†єиКВзВєдЄНеМЕеРЂдїїдљХе≠Чзђ¶дњ°жБѓпЉМжИСжЙАдє†жГѓзЪДtrieж†єиКВзВєеНіжШѓеМЕеРЂдњ°жБѓзЪДпЉМиАМдЄФиЃ§дЄЇињЩж†ЈдєЯжЦєдЊњпЉМдЄЛйЭҐиѓідЄАдЄЛеЃГзЪДжАІиі® (еЯЇдЇОжЬђжЦЗжЙАиЃ®иЃЇзЪДзЃАеНХtrieж†С)
1.¬†¬†¬† е≠Чзђ¶зЪДзІНжХ∞еЖ≥еЃЪжѓПдЄ™иКВзВєзЪДеЗЇеЇ¶пЉМеН≥branchжХ∞зїД(з©ЇйЧіжНҐжЧґйЧіжАЭжГ≥)
2.¬†¬†¬† branchжХ∞зїДзЪДдЄЛж†Здї£и°®е≠Чзђ¶зЫЄеѓєдЇОaзЪДзЫЄеѓєдљНзљЃ
3.¬†¬†¬† йЗЗзФ®ж†ЗиЃ∞зЪДжЦєж≥Хз°ЃеЃЪжШѓеР¶дЄЇе≠Чзђ¶дЄ≤гАВ
4.¬†¬†¬† жПТеЕ•гАБжЯ•жЙЊзЪДе§НжЭВеЇ¶еЭЗдЄЇO(len),lenдЄЇе≠Чзђ¶дЄ≤йХњеЇ¶
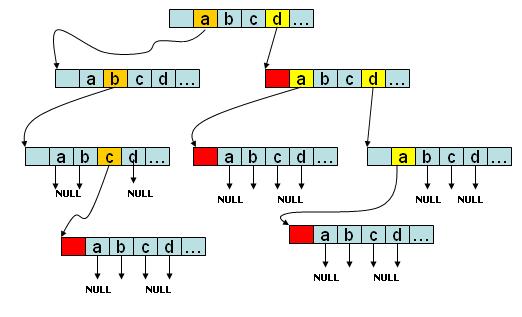
lTrieзЪДз§ЇжДПеЫЊ
 
е¶ВеЫЊжЙАз§ЇпЉМиѓ•trieж†Се≠ШжЬЙabcгАБdгАБdaгАБddaеЫЫдЄ™е≠Чзђ¶дЄ≤пЉМе¶ВжЮЬжШѓе≠Чзђ¶дЄ≤дЉЪеЬ®иКВзВєзЪДе∞ЊйГ®ињЫи°Мж†ЗиЃ∞гАВж≤°жЬЙеРОзї≠е≠Чзђ¶зЪДbranchеИЖжФѓжМЗеРСNULL
lTrieзЪДдЉШзВєдЄЊдЊЛ
еЈ≤зЯ•nдЄ™зФ±е∞ПеЖЩе≠ЧжѓНжЮДжИРзЪДеє≥еЭЗйХњеЇ¶дЄЇ10зЪДеНХиѓН,еИ§жЦ≠еЕґдЄ≠жШѓеР¶е≠ШеЬ®жЯРдЄ™дЄ≤дЄЇеП¶дЄАдЄ™дЄ≤зЪДеЙНзЉАе≠РдЄ≤гАВдЄЛйЭҐеѓєжѓФ3зІНжЦєж≥ХпЉЪ
1.¬†¬†¬† жЬАеЃєжШУжГ≥еИ∞зЪДпЉЪеН≥дїОе≠Чзђ¶дЄ≤йЫЖдЄ≠дїОе§іеЊАеРОжРЬпЉМзЬЛжѓПдЄ™е≠Чзђ¶дЄ≤жШѓеР¶дЄЇе≠Чзђ¶дЄ≤йЫЖдЄ≠жЯРдЄ™е≠Чзђ¶дЄ≤зЪДеЙНзЉАпЉМе§НжЭВеЇ¶дЄЇO(n^2)гАВ
2.¬†¬†¬† дљњзФ®hashпЉЪжИСдїђзФ®hashе≠ШдЄЛжЙАжЬЙе≠Чзђ¶дЄ≤зЪДжЙАжЬЙзЪДеЙНзЉАе≠РдЄ≤гАВеїЇзЂЛе≠ШжЬЙе≠РдЄ≤hashзЪДе§НжЭВеЇ¶дЄЇO(n*len)гАВжߕ胥зЪДе§НжЭВеЇ¶дЄЇO(n)* O(1)= O(n)гАВ
3.¬†¬†¬† дљњзФ®trieпЉЪеЫ†дЄЇељУжߕ胥е¶Ве≠Чзђ¶дЄ≤abcжШѓеР¶дЄЇжЯРдЄ™е≠Чзђ¶дЄ≤зЪДеЙНзЉАжЧґпЉМжШЊзДґдї•b,c,d....з≠ЙдЄНжШѓдї•aеЉАе§ізЪДе≠Чзђ¶дЄ≤е∞±дЄНзФ®жЯ•жЙЊдЇЖгАВжЙАдї•еїЇзЂЛtrieзЪДе§НжЭВеЇ¶дЄЇO(n*len)пЉМиАМеїЇзЂЛ+жߕ胥еЬ®trieдЄ≠жШѓеПѓдї•еРМжЧґжЙІи°МзЪДпЉМеїЇзЂЛзЪДињЗз®ЛдєЯе∞±еПѓдї•жИРдЄЇжߕ胥зЪДињЗз®ЛпЉМhashе∞±дЄНиГљеЃЮзО∞ињЩдЄ™еКЯиГљгАВжЙАдї•жАїзЪДе§НжЭВеЇ¶дЄЇO(n*len)пЉМеЃЮйЩЕжߕ胥зЪДе§НжЭВеЇ¶еП™жШѓO(len)гАВ
 
package trie;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
public class Trie {
 private Vertex root;
 protected class Vertex {
  protected int words;
  protected int prefixes;
  protected Vertex[] edges;
  Vertex() {
   words = 0;
   prefixes = 0;
   edges = new Vertex[26];
   for (int i = 0; i < edges.length; i++) {
    edges[i] = null;
   }
  }
 }
 public Trie() {
  root = new Vertex();
 }
 /** */
 /**
  *
  * List all words in the Trie.
  *
  *
  *
  * @return
  *
  */
 public List<String> listAllWords() {
  List<String> words = new ArrayList<String>();
  Vertex[] edges = root.edges;
  for (int i = 0; i < edges.length; i++) {
   if (edges[i] != null) {
    // System.out.println("test");
    String word = "" + (char) ('a' + i);
    depthFirstSearchWords(words, edges[i], word);
   }
  }
  return words;
 }
 public int countPrefixes(String prefix) {
  return countPrefixes(root, prefix);
 }
 private int countPrefixes(Vertex vertex, String prefixSegment) {
  if (prefixSegment.length() == 0) { // reach the last character of the
   // word
   return vertex.prefixes;
  }
  char c = prefixSegment.charAt(0);
  int index = c - 'a';
  if (vertex.edges[index] == null) { // the word does NOT exist
   return 0;
  } else {
   return countPrefixes(vertex.edges[index], prefixSegment
     .substring(1));
  }
 }
 public int countWords(String word) {
  return countWords(root, word);
 }
 private int countWords(Vertex vertex, String wordSegment) {
  if (wordSegment.length() == 0) { // reach the last character of the
   // word
   return vertex.words;
  }
  char c = wordSegment.charAt(0);
  int index = c - 'a';
  if (vertex.edges[index] == null) { // the word does NOT exist
   return 0;
  } else {
   return countWords(vertex.edges[index], wordSegment.substring(1));
  }
 }
 /** */
 /**
  *
  * Depth First Search words in the Trie and add them to the List.
  *
  *
  *
  * @param words
  *
  * @param vertex
  *
  * @param wordSegment
  *
  */
 private void depthFirstSearchWords(List<String> words, Vertex vertex,
   String wordSegment) {
  Vertex[] edges = vertex.edges;
  boolean hasChildren = false;
  for (int i = 0; i < edges.length; i++) {
   if (edges[i] != null) {
    hasChildren = true;
    String newWord = wordSegment + (char) ('a' + i);
    depthFirstSearchWords(words, edges[i], newWord);
   }
  }
  if (!hasChildren) {
   words.add(wordSegment);
  }
 }
 /** */
 /**
  *
  * Add a word to the Trie.
  *
  *
  *
  * @param word
  *            The word to be added.
  *
  */
 public void addWord(String word) {
  addWord(root, word);
 }
 /** */
 /**
  *
  * Add the word from the specified vertex.
  *
  * @param vertex
  *            The specified vertex.
  *
  * @param word
  *            The word to be added.
  *
  */
 private void addWord(Vertex vertex, String word) {
  if (word.length() == 0) { // if all characters of the word has been
   // added
   vertex.words++;
  } else {
   vertex.prefixes++;
   char c = word.charAt(0);
   c = Character.toLowerCase(c);
   int index = c - 'a';
   if (vertex.edges[index] == null) { // if the edge does NOT exist
    vertex.edges[index] = new Vertex();
   }
   addWord(vertex.edges[index], word.substring(1)); // go the the
   // next
   // character
  }
 }
 public static void main(String args[]) // Just used for test
 {
  Trie trie = new Trie();
  trie.addWord("China");
  trie.addWord("crawl");
  trie.addWord("crime");
  trie.addWord("ban");
  trie.addWord("english");
  trie.addWord("establish");
  trie.addWord("eat");
  List<String> list = trie.listAllWords();
  Iterator listiterator = list.listIterator();
  while (listiterator.hasNext())
  {
   String s = (String) listiterator.next();
   System.out.println(s);
  }
  int count = trie.countPrefixes("c");
  System.out.println("the count of c prefixes:" + count);
 }
}
- 2011-10-26 15:29
- жµПиІИ 848
- иѓДиЃЇ(0)
- еИЖз±ї:зЉЦз®Лиѓ≠и®А
- жЯ•зЬЛжЫіе§Ъ
еПСи°®иѓДиЃЇ
-
жЦ∞еНЪеЉАеРѓ
2013-10-17 11:29 625姩洃䪳жЮЂпЉЪhttp://www.tianyalinfeng ... -
дљњзФ®FileUtilsиОЈеПЦжЦЗдїґе§єдЄЛжЙАжЬЙжМЗеЃЪжЦЗдїґ
2013-09-23 11:42 1546org.apache.commons.io.FileUt ... -
hibernateеОїйЗНе§НжХ∞жНЃ
2013-09-21 19:16 883DetachedCriteria dc = Detached ... -
ckeditorзЃАеНХеЇФзФ®
2013-09-13 11:35 818еЗЖе§З ckeditorеЙНзЂѓжЇРз†Бckeditor_4.2_f ... -
жЈ±еЇ¶е§НеИґ
2013-09-11 16:50 712жµЕе§НеИґпЉЪе∞ЖдЄАдЄ™еѓєи±°е§НеИґеРОпЉМеЯЇжЬђжХ∞жНЃз±їеЮЛзЪДеПШйЗПйГљдЉЪйЗНжЦ∞еИЫеїЇпЉМиАМ ... -
JavaзЪД23дЄ≠иЃЊиЃ°ж®°еЉП
2013-09-10 14:59 1127JavaзЪД23дЄ≠иЃЊиЃ°ж®°еЉП дїОињЩдЄАеЭЧеЉАеІЛпЉМжИСдїђиѓ¶зїЖдїЛзїНJav ... -
иЃЊиЃ°ж®°еЉПзЪДеЕ≠е§ІеОЯеИЩ
2013-09-10 14:51 853иЃЊиЃ°ж®°еЉПзЪДеЕ≠е§ІеОЯеИЩ 1гАБеЉАйЧ≠еОЯеИЩпЉИOpen Close ... -
heritrix-3.1.1зЃАеНХдљњзФ®
2013-09-06 16:43 9191.дЄЛиљљheritrix-3.1.1-dist.zipпЉИж≠§ ... -
webз®ЛеЇПз¶Бж≠ҐиЃњйЧЃжМЗеЃЪжЦЗдїґ
2013-09-04 13:26 754еЬ®web.xmlдЄ≠жЈїеК†е¶ВдЄЛдї£з†БпЉЪ <security ... -
iframeйЗМеПЦдЄНеИ∞struts2 actionйЗМзЪДеАЉ
2013-08-06 11:23 1147struts actionйЗМзЪДе±ЮжАІеАЉж≠£еЄЄйГљжШѓе≠ШжФЊеЬ®reque ... -
struts2дљњзФ®UrlRewriteFilterжЧґжК•йФЩ
2013-07-29 11:18 639struts2дљњзФ®UrlRewriteFilterжЧґжК•йФЩ ... -
javaж≠£еИЩеОїжОЙжЙАжЬЙhtmlж†Зз≠Њ
2013-07-02 14:40 880public static String trimHtml( ... -
javaз±їдЄ≠иОЈеПЦclassesжЦЗдїґе§єиЈѓеЊД
2013-07-02 14:20 1023дЊЛе¶ВпЉЪTest.java еЬ®TestдЄ≠иОЈеПЦй°єзЫЃclasse ... -
EhcacheйЕНзљЃ
2013-07-01 15:41 834<defaultCache             ... -
jspдЄ≠ <%! %> еТМ <% %> зЪДеМЇеИЂ
2013-05-22 15:35 594<%! int a = 0; %> ¬† ељУjs ... -
зФ®йАТељТеЃЮзО∞жЯ•жЙЊжЬАе§ІеАЉ
2013-05-14 11:42 540private static int recursiveM ... -
еЄЄзФ®ж≠£еИЩи°®иЊЊеЉП
2013-05-07 16:11 488/** * check mobile phone num ... -
дЄ≠жЦЗиљђжЛЉйЯ≥
2013-05-02 15:35 453import net.sourceforge.pinyin4 ... -
javaиОЈеПЦжЯРдЄАеєіжЯРдЄ™иКВж∞ФжЧ•жЬЯ
2013-04-27 15:43 1908private static String[] solar ... -
еЕђеОЖеЖЬеОЖдЇТзЫЄиљђжНҐ
2013-04-26 10:08 1038public class CalendarUtil { / ...







зЫЄеЕ≥жО®иНР
### ITзђФиѓХйЭҐиѓХ--Trieж†СпЉИеЙНзЉАж†СпЉЙеЄЄиАГйҐШзЫЃеПКиІ£жЮР #### ж¶Вињ∞ Trieж†СпЉМеПИзІ∞е≠ЧеЕЄж†СжИЦеЙНзЉАж†СпЉМжШѓдЄАзІНзФ®дЇОењЂйАЯж£А糥зЪДе§ЪеПЙж†СзїУжЮДпЉМеєњж≥ЫеЇФзФ®дЇОе≠Чзђ¶дЄ≤е§ДзРЖйҐЖеЯЯгАВеЃГиГљжЬЙжХИеЬ∞еИ©зФ®е≠Чзђ¶дЄ≤зЪДеЕђеЕ±еЙНзЉАжЭ•еЗПе∞Се≠ШеВ®з©ЇйЧіпЉМеєґеЬ®жߕ胥...
### Trieж†СеЃЮзО∞иѓ¶иІ£ #### дЄАгАБTrieж†СзЃАдїЛ Trieж†СпЉМдєЯзІ∞дЄЇеЙНзЉАж†СжИЦе≠ЧеЕЄж†СпЉМжШѓдЄАзІНзФ®дЇОе≠ШеВ®е≠Чзђ¶дЄ≤жХ∞жНЃзїУжЮДгАВеЃГеИ©зФ®е≠Чзђ¶дЄ≤йЧізЪДеЕђеЕ±еЙНзЉАжЭ•еЗПе∞СжЙАйЬАзЪДе≠ШеВ®з©ЇйЧіпЉМдљњеЊЧжЯ•жЙЊе≠Чзђ¶дЄ≤жЫіеК†йЂШжХИгАВTrieж†СеЬ®еЊИе§ЪеЇФзФ®дЄ≠йГљжЬЙеєњж≥ЫзЪД...
"Trieж†СеЕ•йЧ®пЉМеЊИеЃєжШУдЄКжЙЛ" Trieж†СжШѓдЄАзІНж†С嚥зїУжЮДпЉМзФ®дЇОдњЭе≠Ше§ІйЗПзЪДе≠Чзђ¶дЄ≤гАВеЃГзЪДдЉШзВєжШѓпЉЪеИ©зФ®е≠Чзђ¶дЄ≤зЪДеЕђеЕ±еЙНзЉАжЭ•иКВзЇ¶е≠ШеВ®з©ЇйЧігАВзЫЄеѓєжЭ•иѓіпЉМTrieж†СжШѓдЄАзІНжѓФиЊГзЃАеНХзЪДжХ∞жНЃзїУжЮДгАВзРЖиІ£иµЈжЭ•жѓФиЊГзЃАеНХпЉМдљЖжШѓзЃАеНХзЪДдЄЬи•њдєЯеЊЧдїШеЗЇ...
дЄАдЄ™зЃАеНХзЪДCиѓ≠и®Аз®ЛеЇПпЉЪзФ®Trieж†СеЃЮзО∞иѓНйҐСзїЯиЃ°еТМеНХиѓНжߕ胥
ињЩдЄ™й°єзЫЃвАЬеЯЇдЇОTrieж†Сж®°дїњи∞Јж≠МзЩЊеЇ¶жРЬ糥ж°ЖжПРз§ЇвАЭжЧ®еЬ®еЃЮзО∞з±їдЉЉи∞Јж≠МеТМзЩЊеЇ¶жРЬ糥еЉХжУОзЪДиЗ™еК®и°•еЕ®еКЯиГљгАВжИСдїђе∞ЖжЈ±еЕ•жОҐиЃ®Trieж†СжХ∞жНЃзїУжЮДдї•еПКе¶ВдљХдљњзФ®JavaжЭ•жЮДеїЇињЩж†ЈзЪДз≥їзїЯгАВ й¶ЦеЕИпЉМжИСдїђи¶БзРЖиІ£дїАдєИжШѓTrieж†СпЉМдєЯ襀зІ∞дЄЇеЙНзЉАж†СжИЦ...
trie.cдЄ≠еЃЪдєЙдЇЖtrieж†СзЪДжУНдљЬеЗљжХ∞пЉЫ trie.hдЄЇзЫЄеЇФзЪДе§іжЦЗдїґпЉЫ test.cзФ®дЇОжµЛиѓХзЫЄеЕ≥зЪДеЗљжХ∞гАВ еЬ®trie.cдЄ≠пЉМеЕ≥дЇОжЯ•жЙЊеЃЪдєЙдЇЖдЄ§дЄ™еЗљжХ∞пЉМдЄАдЄ™жШѓfind()пЉМдЄАдЄ™жШѓsearch()пЉМдЇМиАЕзЪДеМЇеИЂжШѓпЉМеЙНиАЕдїЕеИ§жЦ≠дЄАдЄ™е≠Чзђ¶дЄ≤жШѓеР¶еЬ®ж†СдЄ≠еЗЇзО∞пЉМ...
зФ®PythonеЃЮзО∞Trieж†СзЪДеЇФзФ®пЉМеєґеПѓдї•еѓєиЛ±ж±ЙиѓНеЕЄињЫи°МеѓЉеЕ•еТМж£А糥гАБжЈїеК†еТМеИ†йЩ§пЉМжЬАзїИеПѓдї•е∞ЖеѓЉеЕ•зЪДиЛ±ж±ЙиѓНеЕЄдњЭе≠ШеИ∞жЬђеЬ∞з£БзЫШгАВеЖЕйЩДдЄ§дЄ™.pyжЦЗдїґпЉМеИЖеИЂжШѓtree.pyеТМd_gui.pyпЉМtree.pyжШѓз±їеТМжЦєж≥Х,d_gui.pyжШѓеی嚥зХМйЭҐпЉЫдЄАдЄ™.txt...
зФ®CеЃЮзО∞зЪДжХ∞жНЃзїУжЮДTrieж†СзЃЧж≥Х еЃЮй™МзЪДеЗљжХ∞зЪДtrieж†СзЪДжПТеЕ• жРЬ糥еТМеИ†йЩ§
### ACM Trieж†Сиѓ¶иІ£ #### дЄАгАБTrieж†СзЪДеЯЇжЬђж¶Вењµ **Trieж†С**пЉМеПИзІ∞дЄЇ**е≠ЧеЕЄж†С**жИЦ**еЙНзЉАж†С**пЉМжШѓдЄАзІНзФ®дЇОйЂШжХИе≠ШеВ®еТМж£А糥е≠Чзђ¶дЄ≤зЪДж†С嚥жХ∞жНЃзїУжЮДгАВеЃГйАЪињЗеИ©зФ®е≠Чзђ¶дЄ≤дєЛйЧізЪДеЕђеЕ±еЙНзЉАжЭ•еЗПе∞Сжߕ胥жЧґйЧіпЉМдїОиАМжПРйЂШжРЬ糥жХИзОЗгАВ...
гАРTrieж†СгАС Trieж†СпЉМеПИзІ∞дЄЇе≠ЧеЕЄж†СпЉМжШѓдЄАзІНзЙєжЃКзЪДж†С嚥жХ∞жНЃзїУжЮДпЉМдЄїи¶БзФ®дЇОйЂШжХИеЬ∞е≠ШеВ®еТМж£А糥е≠Чзђ¶дЄ≤гАВеЃГзЪДиЃЊиЃ°зЫЃзЪДжШѓйАЪињЗеИ©зФ®е≠Чзђ¶дЄ≤зЪДеЕђеЕ±еЙНзЉАжЭ•еЗПе∞Се≠Чзђ¶дЄ≤жѓФиЊГзЪДжђ°жХ∞пЉМдїОиАМжПРйЂШжߕ胥жХИзОЗгАВTrieж†СзЪДж†ЄењГзЙєзВєжШѓпЉЪ 1. ж†є...
**еУИеЄМ Trie ж†СпЉИHashTrieпЉЙдЄОе≠ЧеЕЄж†СпЉИTrieж†СпЉЙиѓ¶иІ£** еУИеЄМ Trie ж†СпЉМдєЯзІ∞дЄЇ HashTrie жИЦиАЕжШѓеУИеЄМеМЦзЪД Trie ж†СпЉМжШѓдЄАзІНзїУеРИдЇЖеУИеЄМи°®еТМ Trie жХ∞жНЃзїУжЮДзЙєзВєзЪДжХ∞жНЃзїУжЮДгАВеЃГеЬ® Trie ж†СзЪДеЯЇз°АдЄКеЉХеЕ•дЇЖеУИеЄМеЗљжХ∞пЉМжПРйЂШдЇЖ...
йАЪињЗеЯЇдЇОеИТеИЖдљНжЮДеїЇжЧ†еЖ≤з™БеУИеЄМеЗљжХ∞пЉМеЃЮзО∞еѓєзЙЗдЄКе≠ШеВ®еЩ®жЬЙжХИзЪДжОІеИґпЉМжФїеЗїзЙєеЊБеє≥еЭЗеИЖйЕНеИ∞trieж†СжѓПе±ВзЪДе§ЪдЄ™зїДдЄ≠гАВиѓ•зїУжЮДеПѓдї•еЬ®еРМдЄАдЄ™иКѓзЙЗдЄ≠еЃЮзО∞жµБж∞іеєґи°МеЬ∞жЙІи°МпЉМиОЈеЊЧжѓФиЊГе§ІзЪДеРЮеРРйЗПгАВзРЖиЃЇеПКеЃЮй™Ми°®жШОиѓ•жЦєж≥ХеЬ®зЙЗдЄКе≠ШеВ®еЩ®дЄА...
е≠ЧеЕЄж†СпЉМдєЯ襀зІ∞дЄЇTrieж†СжИЦеЙНзЉАж†СпЉМжШѓдЄАзІНйЂШжХИзЪДжХ∞жНЃзїУжЮДпЉМе∞§еЕґйАВзФ®дЇОе≠Чзђ¶дЄ≤зЫЄеЕ≥зЪДжЯ•жЙЊеТМжПТеЕ•жУНдљЬгАВеЬ®иЃ°зЃЧжЬЇзІСе≠¶йҐЖеЯЯпЉМеЃГ襀府ж≥ЫеЇФзФ®еЬ®е≠ЧеЕЄгАБжРЬ糥еЉХжУОгАБиЗ™еК®и°•еЕ®еКЯиГљдї•еПКIPиЈѓзФ±з≠ЙжЦєйЭҐгАВTrieж†СзЪДж†ЄењГдЉШеКњеЬ®дЇОеЕґиГље§ЯйАЪињЗ...
"Trieж†СпЉИе≠ЧеЕЄж†СпЉЙеЯЇжЬђеОЯзРЖ" Trie ж†СпЉМдєЯзІ∞дЄЇе≠ЧеЕЄж†СпЉМжШѓдЄАзІНж†С嚥жХ∞жНЃзїУжЮДпЉМзФ®дЇОйЂШжХИе≠ШеВ®еТМжߕ胥е≠Чзђ¶дЄ≤гАВеЕґж†ЄењГжАЭжГ≥жШѓз©ЇйЧіжНҐжЧґйЧіпЉМеН≥йАЪињЗеН†зФ®жЫіе§ЪзЪДе≠ШеВ®з©ЇйЧіжЭ•жНҐеПЦжߕ胥йАЯеЇ¶зЪДжПРйЂШгАВ Trie ж†СзЪДеЯЇжЬђзїУжЮДжШѓдЄАдЄ™иКВзВєжХ∞зїД...
гАРTrieж†СйҐШиІ£1гАС Trieж†СпЉМеПИзІ∞е≠ЧеЕЄж†СжИЦеЙНзЉАж†СпЉМжШѓдЄАзІНзФ®дЇОйЂШжХИе≠ШеВ®еТМж£А糥е≠Чзђ¶дЄ≤зЪДжХ∞жНЃзїУжЮДгАВеЃГзЪДдЄїи¶БзЙєзВєжШѓиГље§ЯењЂйАЯжЯ•жЙЊдЄАдЄ™е≠Чзђ¶дЄ≤жШѓеР¶жШѓеП¶дЄАдЄ™е≠Чзђ¶дЄ≤зЪДеЙНзЉАпЉМињЩеѓєдЇОе§ДзРЖе§ІйЗПе≠Чзђ¶дЄ≤зЪДйЧЃйҐШйЭЮеЄЄжЬЙзФ®гАВеЬ®йҐШзЫЃжППињ∞дЄ≠...
Trieж†СпЉМдєЯ襀зІ∞дЄЇеЙНзЉАж†СжИЦе≠ЧеЕЄж†СпЉМжШѓдЄАзІНжХ∞жНЃзїУжЮДпЉМдЄїи¶БзФ®дЇОйЂШжХИеЬ∞е≠ШеВ®еТМж£А糥е≠Чзђ¶дЄ≤гАВеЬ®Trieж†СдЄ≠пЉМжѓПдЄ™иКВзВєдї£и°®дЄАдЄ™е≠Чзђ¶дЄ≤зЪДеЙНзЉАпЉМиАМдїОж†єиКВзВєеИ∞жЯРдЄ™иКВзВєзЪДиЈѓеЊДдЄКзЪДиЊєдї£и°®дЇЖињЩдЄ™иКВзВєжЙАдї£и°®зЪДе≠Чзђ¶дЄ≤гАВињЩзІНзїУжЮДзЙєеИЂйАВеРИ...
**DoubleArrayTrieпЉИеПМжХ∞зїДTrieж†СпЉЙиѓ¶иІ£** DoubleArrayTrieпЉИзЃАзІ∞DATпЉЙпЉМжШѓдЄАзІНйЂШжХИзЪДжХ∞жНЃзїУжЮДпЉМеЄЄзФ®дЇОе≠Чзђ¶дЄ≤зЪДжЯ•жЙЊеТМеМєйЕНпЉМзЙєеИЂжШѓеЬ®еИЖиѓНж£А糥гАБжХ∞жНЃжМЦжОШдї•еПКжРЬ糥еЉХжУОз≠ЙйҐЖеЯЯжЬЙзЭАеєњж≥ЫзЪДеЇФзФ®гАВеЃГжШѓзФ±жЧ•жЬђе≠¶иАЕйЂШжі•йЩµ...
### еПМжХ∞зїДTrieж†СзЃЧж≥ХдЉШеМЦеПКеЕґеЇФзФ®з†Фз©ґ #### жСШи¶БдЄОеЕ≥йФЃиѓНиІ£жЮР жЬђжЦЗдЄїи¶БжОҐиЃ®дЇЖдЄАзІНйТИеѓєеПМжХ∞зїДTrieж†СпЉИDouble-Array TrieпЉЙзЃЧж≥ХзЪДдЉШеМЦз≠ЦзХ•пЉМеєґйАЪињЗеЃЮй™Мй™МиѓБдЇЖиѓ•з≠ЦзХ•зЪДжЬЙжХИжАІгАВеПМжХ∞зїДTrieж†СжШѓдЄАзІНйЂШжХИзЪДжХ∞жНЃзїУжЮДпЉМеЄЄ...
### еЃЮзО∞Trieж†СзЪДC/C++ж®°жЭњ еЬ®иЃ°зЃЧжЬЇзІСе≠¶йҐЖеЯЯпЉМTrieж†СпЉИеПИзІ∞еЙНзЉАж†СжИЦе≠ЧеЕЄж†СпЉЙжШѓдЄАзІНзФ®дЇОе≠ШеВ®еЕЈжЬЙеЕ±еРМеЙНзЉАзЪДе≠Чзђ¶дЄ≤зЪДйЂШжХИжХ∞жНЃзїУжЮДгАВеЃГеєњж≥ЫеЇФзФ®дЇОеРДзІНеЬЇжЩѓпЉМе¶ВиЗ™еК®и°•еЕ®гАБжЛЉеЖЩж£АжЯ•дї•еПКIPиЈѓзФ±и°®з≠ЙгАВжЬђжЦЗе∞Жиѓ¶зїЖдїЛзїНе¶ВдљХ...
Trieж†СпЉМеПИзІ∞еЙНзЉАж†СжИЦе≠ЧеЕЄж†СпЉМжШѓдЄАзІНзФ®дЇОе≠ШеВ®е≠Чзђ¶дЄ≤зЪДжХ∞жНЃзїУжЮДпЉМеЃГеЬ®ITйҐЖеЯЯе∞§еЕґжШѓжХ∞жНЃзїУжЮДеТМзЃЧж≥ХзЪДе≠¶дє†дЄ≠еН†жНЃзЭАйЗНи¶БзЪДеЬ∞дљНгАВињЩдЄ™еОЛзЉ©еМЕеМЕеРЂзЪДвАЬзОЛиµЯ.docвАЭеТМвАЬзОЛиµЯ.pptвАЭеЊИеПѓиГљжШѓеЕ≥дЇОTrieж†СзЪДиѓ¶зїЖиЃ≤иІ£еТМеЃЮиЈµйҐШзЫЃпЉМ...