`

学习笔记——最小二乘法

 
阅读更多

1、最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配

2、典型的一类函数模型是线性函数模型。最简单的线性式是y = x0 + x1t，写成行列式，为

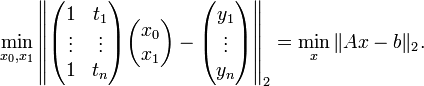
\min_{x_0,x_1}\left\|\begin{pmatrix}1 & t_1 \\ \vdots & \vdots \\ 1 & t_n \end{pmatrix} \begin{pmatrix} x_0\\ x_1\end{pmatrix} - \begin{pmatrix} y_1 \\ \vdots \\ y_{n}\end{pmatrix}\right\|_{2} = \min_x\|Ax-b\|_2.

直接给出该式的参数解：

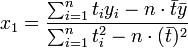x_1 = \frac{\sum_{i=1}^n t_iy_i - n \cdot \bar t \bar y}{\sum_{i=1}^n t_i^2- n \cdot (\bar t)^2} 和 x_0 = \bar y - x_1 \bar t

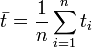其中\bar t = \frac{1}{n} \sum_{i=1}^n t_i，为t值的算术平均值。也可解得如下形式：

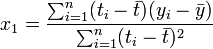
x_1 = \frac{\sum_{i=1}^n (t_i - \bar t)(y_i - \bar y)}{\sum_{i=1}^n (t_i - \bar t)^2}

3、简单线性模型 y = a+ bx 的例子

 

4、最小二乘是一种最基本的辨识方法，但它具有两方面的缺陷：

  1. 当模型噪声是有色噪声时，最小二乘估计不是无偏、一致估计；
  2. 随着数据的增长，将出现所谓的“数据饱和”现象。

针对这两个问题，出现了相应的辨识算法，如遗忘因子法、限定记忆法、偏差补偿法、增广最小二乘、广义最小二乘、辅助变量法、二步法及多级最小二乘法等。

分享到：
| 使用StringTokenizer统计文本行单词个数
评论
发表评论

您还没有登录,请您登录后再发表评论

相关推荐

    数学建模学习笔记——常见的预测模型总结

    GM(1, 1)模型适用于数据呈现近似指数增长的序列，它通过一次累加生成序列和均值生成序列，建立灰微分方程，然后通过最小二乘法求解模型参数。预测过程包括数据检验、模型建立、预测值计算及预测值检验等步骤。对于非...

    自写线代笔记——李永乐.pdf

    6. 正交性和最小二乘法：正交向量和正交矩阵的概念，最小二乘法在数据拟合中的应用。 7. 线性变换：线性变换的定义、性质和矩阵表示。理解线性变换与向量空间之间的关系。 考研学生在准备考试时，需要系统地学习...

    斯坦福大学公开课机器学习笔记

    【机器学习笔记——斯坦福大学公开课】 机器学习是人工智能领域的一个重要分支，它涉及如何让计算机从数据中学习规律，并运用这些规律进行预测和决策。本笔记基于斯坦福大学的机器学习公开课，主要讨论了线性回归、...

    机器学习笔记

    ### 机器学习笔记之回归方法详解 #### 一、引言 本文档是对斯坦福大学机器学习课程前四节的学习总结及深入理解。本部分主要关注回归问题——一种常见的有监督学习方法。回归方法旨在从有限的数据集中推导出一个数学...

    人大统计学院—高维数据处理详细笔记（1）——概率论基础

    在实际应用中，我们通常假设误差项满足正态分布，这使得我们可以使用最大似然估计或最小二乘法来估计模型参数。 在高维数据处理中，面对大量的特征，我们可能会遇到维度灾难问题，这使得模型过拟合或训练数据不足。...

    斯坦福机器学习网页转pdf版本01-05

    这部分内容会讲解如何通过线性方程来拟合数据，包括最小二乘法的原理以及如何求解参数。它还会讨论残差、误差和预测的概念，以及如何通过R²分数评估模型的性能。此外，可能会涉及线性回归的假设，如独立性、同方差...

    现控ppt.rar西交考研考研用

    辨识方法包括最小二乘法、递归最小二乘等，它们为系统分析和控制设计提供基础。 这个压缩包中的PPT可能包含了上述各个知识点的详细讲解，配以图表和实例，帮助考生直观地理解抽象的控制理论。复习时，考生可以结合...

Magicbox
Global site tag (gtag.js) - Google Analytics