菜鸟笔记——Pearson关系系数

皮尔逊相关系数理解有两个角度

其一, 按照高中数学水平来理解, 它很简单, 可以看做将两组数据首先做Z分数处理之后, 然后两组数据的乘积和除以样本数

Z分数一般代表正态分布中, 数据偏离中心点的距离.等于变量减掉平均数再除以标准差.(就是高考的标准分类似的处理)

标准差则等于变量减掉平均数的平方和,再除以样本数,最后再开方.

所以, 根据这个最朴素的理解,我们可以将公式依次精简为:

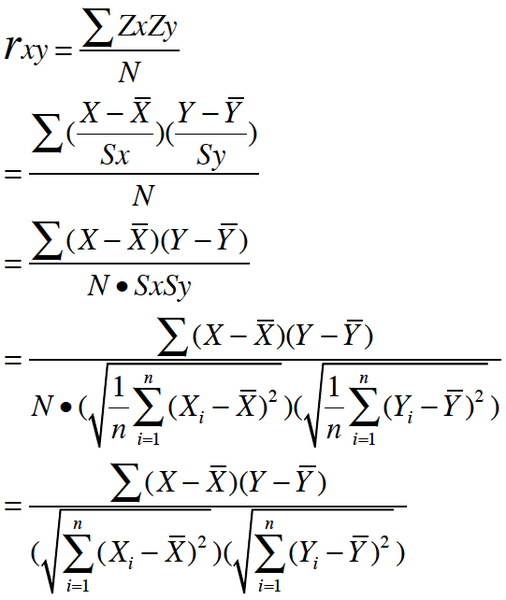
其二, 按照大学的线性数学水平来理解, 它比较复杂一点,可以看做是两组数据的向量夹角的余弦.

皮尔逊相关的约束条件

从以上解释, 也可以理解皮尔逊相关的约束条件:

• 1 两个变量间有线性关系

• 2 变量是连续变量

• 3 变量均符合正态分布,且二元分布也符合正态分布

• 4 两变量独立

在实践统计中,一般只输出两个系数,一个是相关系数,也就是计算出来的相关系数大小,在-1到1之间;另一个是独立样本检验系数,用来检验样本一致性.

先举个手算的例子

使用维基中的例子:

例如，假设五个国家的国民生产总值分别是1、2、3、5、8（单位10亿美元），又假设这五个国家的贫困比例分别是11%、12%、13%、15%、18%。

创建2个向量.(R语言)

x<-c(1,2,3,5,8)

y<-c(0.11,0.12,0.13,0.15,0.18)

按照维基的例子,应计算出相关系数为1出来.我们看看如何一步一步计算出来的.

x的平均数是:3.8
y的平均数是0.138
所以,

sum((x-mean(x))*(y-mean(y)))=0.308

用大白话来写就是:

(1-3.8)*(0.11-0.138)=0.0784
(2-3.8)*(0.12-0.138)=0.0324
(3-3.8)*(0.13-0.138)=0.0064
(5-3.8)*(0.15-0.138)=0.0144
(8-3.8)*(0.18-0.138)=0.1764

0.0784+0.0324+0.0064+0.0144+0.1764=0.308

同理, 分号下面的,分别是:

sum((x-mean(x))^2)=30.8
sum((y-mean(y))^2)= 0.00308

用大白话来写,分别是:

(1-3.8)^2=7.84 #平方
(2-3.8)^2=3.24 #平方
(3-3.8)^2=0.64 #平方
(5-3.8)^2=1.44 #平方
(8-3.8)^2=17.64 #平方

7.84+3.24+0.64+1.44+17.64=30.8

同理,求得:

sum((y-mean(y))^2)= 0.00308

然后再开平方根,分别是:

30.8^0.5=5.549775
0.00308^0.5=0.05549775

用分子除以分母,就计算出最终结果:

0.308/(5.549775*0.05549775)=1

• 再举个简单的R语言例子(R在这里下载: http://cran.r-project.org/bin/macosx/)

假设有100人, 一组数据是年龄,平均年龄是35岁,标准差是5岁;另一组数据是发帖数量,平均帖子数量是45份post,标准差是8份帖子.

假设这两组都是正态分布.我们来求这两者的皮尔逊相关系数,R脚本如下:

> x<-rnorm(n=100,mean=35,sd=5)  #创建一组平均数为35,标准差为5,样本数为100的随机数

> y<-rnorm(n=100,mean=45,sd=8) #创建一组平均数为45,标准差为8,样本数为100的随机数

>  cor.test(x,y,method="pearson") #计算这两组数的相关,并进行T检验

然后R输出结果为:

Pearson's product-moment correlation



data:  x and y

t = -0.0269, df = 98, p-value = 0.9786

alternative hypothesis: true correlation is not equal to 0

95 percent confidence interval:

 -0.1990316  0.1938019

sample estimates:

         cor

-0.002719791

当然,这里是随机数.也可以用非随机的验证一下计算.

皮尔逊相关系数用于网站开发

直接将R与Ruby关联起来

调用很简单,仿照上述例子:

cor(x,y)

就输出系数结果了.

有这么几个库可以参考:

https://github.com/alexgutteridge/rsruby

https://github.com/davidrichards/stat...

https://github.com/jtprince/simpler

说明, 以上为ruby调用库. pythone程序员可以参考: Rpy (http://rpy.sourceforge.net/)

简单的相关系数的分类

• 0.8-1.0 极强相关
• 0.6-0.8 强相关
• 0.4-0.6 中等程度相关
• 0.2-0.4 弱相关
• 0.0-0.2 极弱相关或无相关

ps : 这个网站开发者不要再次发明轮子,本来用markdown语法写作很爽,结果又不得不花时间来改动.请考虑尽快支持Markdown语法.