еОЯжЦЗиљђиЗ™пЉЪhttp://www.matrix67.com/blog/archives/4324
 
 
дЄКеЄЭеИЫйА†дЇЖжХіжХ∞пЉМеЕґдљЩзЪДеИЩжШѓжИСдїђдЇЇз±їзЪДдЇЛдЇЖгАВж≠£еЫ†дЄЇе¶Вж≠§пЉМиі®жХ∞гАБеЃМеЕ®жХ∞гАБFibonacci жХ∞дєЛз±їзЪДжХ∞еИЧжЙНдЉЪиЃ©жХ∞е≠¶еЃґдїђе¶ВзЧіе¶ВйЖЙпЉМеЫ†дЄЇеЃГдїђзЪДе≠ШеЬ®жШѓе¶Вж≠§иЗ™зДґпЉМж≤°жЬЙдїїдљХдЇЇйА†зЪДеЫ†зі†гАВдЇЛеЃЮдЄКпЉМжХ∞е≠¶еЃґдїђеѓєињЩдЇЫжХ∞зЪДиЃ§иѓЖдєЯиґКжЭ•иґКдЄ∞еѓМпЉМжМЦжОШеЗЇдЇЖињЩдЇЫжХ∞еИЧдЄ≠иґКжЭ•иґКжЈ±еИїзЪДжАІиі®гАВ
¬†¬†¬†¬†дЄНињЗпЉМдЇЇз±їз°ЃеЃЮ姙檯е∞ПдЇЖгАВињШжЬЙе•ље§ЪжЮДйА†еЉВеЄЄзЃАеНХзЪДвАЬ篃姩зДґжХ∞еИЧвАЭпЉМжИСдїђдЇЖиІ£еЊЧеЃЮеܮ姙е∞СгАВKolakoski жХ∞еИЧе∞±жШѓжЬАе•љзЪДдЊЛе≠РдєЛдЄАгАВ
¬†¬†¬†¬†Kolakoski жХ∞еИЧдїЕзФ± 1 еТМ 2 жЮДжИРпЉМеЕґдЄ≠е§і 100 дЄ™жХ∞жШѓ
1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1,
2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1,
1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2,
2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, ...
¬†¬†¬†¬†е¶ВжЮЬжИСдїђжККињЮзї≠зЪДзЫЄеРМжХ∞зЬЛдљЬдЄАзїДзЪДиѓЭпЉМжХідЄ™жХ∞еИЧзЪДеЃЪдєЙе∞±еП™жЬЙдЄ§еП•иѓЭпЉЪ a(1) = 1 пЉМ a(n) и°®з§Їзђђ n зїДжХ∞зЪДйХњеЇ¶гАВдЊЛе¶ВпЉМa(6)
= 2пЉМе∞±и°®жШОзђђ 6 зїДжХ∞пЉИдїОзђђ 8 дЄ™жХ∞зЃЧиµЈпЉЙзЪДйХњеЇ¶е∞±жШѓ 2гАВж≥®жДПпЉМжЬЙдЇЖињЩеЗ†дЄ™жЭ°дїґпЉМжХідЄ™еЇПеИЧе∞±еЈ≤зїПеФѓдЄАеЬ∞з°ЃеЃЪдЇЖпЉБa(1) = 1
е∞±и°®жШОзђђдЄАзїДжХ∞еП™жЬЙдЄАдЄ™жХ∞пЉМеЫ†ж≠§дЄЛдЄАдЄ™жХ∞ењЕй°їи¶БжНҐжИР 2 пЉМеЫ†ж≠§ a(2) = 2 пЉЫиАМ a(2) = 2 еПИиѓіжШОињЩдЄ™ 2 ењЕй°їи¶БињЮзЭАеЗЇзО∞дЄ§дЄ™пЉМеЫ†ж≠§
a(3) = 2пЉЫиАМ a(3) = 2 е∞±и°®жШОжХ∞еИЧжО•дЄЛжЭ•и¶БжЬЙдЄ§дЄ™ 1
пЉМз≠Йз≠ЙгАВдєЯе∞±жШѓиѓіпЉМзФЯжИРињЩдЄ™жХ∞еИЧзЪДвАЬеПВжХ∞вАЭе∞±жШѓињЩдЄ™жХ∞еИЧжЬђиЇЂгАВжЫійЕЈзЪДиѓіж≥ХеИЩжШѓпЉМињЩдЄ™жХ∞еИЧжШѓеИЖ嚥зЪДпЉЪе¶ВжЮЬжККжѓПдЄАзїДжХ∞зФ®еЃГзЪДйХњеЇ¶жЭ•жЫњжНҐпЉМе∞±дЉЪеЊЧеИ∞ињЩдЄ™жХ∞еИЧжЬђ
иЇЂгАВеП¶е§ЦдЄАдЄ™еПѓиГљжЬЙдЇЫеЗЇдЇЇжДПжЦЩзЪДдЇЛеЃЮжШѓпЉЪKolakoski жХ∞еИЧеЬ® OEIS дЄ≠зЪДеЇПеПЈйЭЮеЄЄйЭ†еЙНвАФвАФ A000002
гАВ
¬†¬†¬†¬†еЕ≥дЇО Kolakoski жХ∞еИЧпЉМжИСдїђзЯ•йБУдЇЫдїАдєИпЉЯеЊИе∞СгАВжИСдїђзЯ•йБУпЉМињЩдЄ™жХ∞еИЧеПѓдї•зФ®йАТељТеЉП a(a(1) + a(2) + ... + a(k)) = (3 + (-1)k
)/2 жЭ•и°®иЊЊгАВжИСдїђзЫЃеЙНеЈ≤зїПзЯ•йБУпЉМеОїжОЙжХ∞еИЧжЬАеЙНйЭҐзЪД 1пЉМеЙ©дЄЛзЪДйГ®еИЖеПѓдї•дїО 22 еЉАеІЛпЉМзФ±жЫњжНҐиІДеИЩ 22вЖТ2211пЉМ21вЖТ221пЉМ12вЖТ211пЉМ11вЖТ21 ињ≠дї£дЇІзФЯгАВ
¬†¬†¬†¬†Kolakoski жХ∞еИЧзЪДзђђ n
й°єжЬЙйЭЮйАТељТзЪДеЕђеЉПеРЧпЉЯзЫЃеЙНжИСдїђињШдЄНзЯ•йБУгАВеЈ≤зїПеЗЇзО∞ињЗзЪДжХ∞е≠ЧдЄ≤дїКеРОйГљињШдЉЪеЖНжђ°еЗЇзО∞еРЧпЉЯзЫЃеЙНжИСдїђдєЯдЄНзЯ•йБУгАВињШжЬЙпЉМжИСдїђжЬЙзРЖзФ±зМЬжГ≥пЉМжХ∞еИЧдЄ≠ 1 еТМ 2
зЪДдЄ™жХ∞еРДеН†дЄАеНКгАВдЄЛеЫЊжШЊз§ЇзЪДе∞±жШѓжХ∞еИЧеЙН n й°єдЄ≠жХ∞е≠Ч 1 жЙАеН†зЪДжѓФдЊЛпЉМеПѓиІБжИСдїђзЪДзМЬжГ≥еЊИеПѓиГљжШѓеѓєзЪДгАВ
    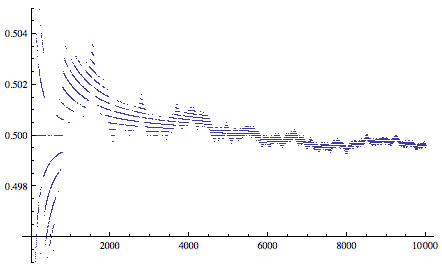
¬†¬†¬†¬†дЄНињЗпЉМзЫЃеЙНињШж≤°жЬЙдЇЇиГље§ЯиѓБжШОињЩдЄАзВєгАВиАМжЬАињСзЪДдЄАдЇЫз†Фз©ґеИЩи°®жШОпЉМжХ∞е≠Ч 1 зЪДжѓФдЊЛеЊИеПѓиГљдЄНжШѓ 1/2 гАВељУзДґпЉМињШжЬЙзђђдЄЙзІНеПѓиГљвАФвАФињЩдЄ™жЮБйЩРеПѓиГљж†єжЬђдЄНе≠ШеЬ®гАВињЩжЧ†зЦСеПИжШѓдЄАдЄ™жЬАжКШз£®дЇЇзЪДжХ∞е≠¶жЬ™иІ£дєЛи∞Ь
гАВ
еИЖдЇЂеИ∞пЉЪ












зЫЄеЕ≥жО®иНР
"йБЧдЉ†зЃЧж≥ХдЉШеМЦзЉЦз†БеЇПеИЧпЉЪеЃЮзО∞иґЕи°®йЭҐRCSзЉ©еЗПзЪДMATLABдЄОPythonеПМдї£з†БиІ£еЖ≥жЦєж°И","йБЧдЉ†зЃЧж≥ХдЉШеМЦзЉЦз†БеЇПеИЧпЉЪеЃЮзО∞иґЕи°®йЭҐRCSзЉ©еЗПзЪДMATLABдЄОPythonеПМдї£з†БиІ£еЖ≥жЦєж°И",йБЧдЉ†зЃЧж≥ХдЉШеМЦзЉЦз†БеЇПеИЧпЉМеЃЮзО∞зЉЦз†БиґЕи°®йЭҐrcsзЉ©еЗПгАВ дљњзФ®MATLAB...
иљђжНҐдЄЇеЫЫеЕГжХ∞еПѓдї•еЄЃеК©жИСдїђйБњеЕНдЄЗеРСйФБйЧЃйҐШпЉМдЄЗеРСйФБжШѓељУињЮзї≠зЪДдЄ§дЄ™жЧЛиљђиљідЇТзЫЄеЮВзЫіжЧґпЉМзђђдЄЙдЄ™иљізЪДжЧЛиљђжЧ†ж≥Хж≠£з°Ѓи°®иЊЊзЪДжГЕеЖµгАВеЫЫеЕГжХ∞жШѓдЄАзІНжЙ©е±ХзЪДе§НжХ∞嚥еЉПпЉМзФ®еЫЫдЄ™еЃЮжХ∞зїДжИРпЉИw, x, y, zпЉЙпЉМеЕґдЄ≠wжШѓеЃЮйГ®пЉМx, y, zжШѓиЩЪйГ®пЉМ...
иѓ¶зїЖдїЛзїНжЬАйХњйАТеЗПе≠РиЃЊжЬЙдЄАдЄ™жХіжХ∞еЇПеИЧA1, A2, ... AnпЉМж±ВињЩдЄ™еЇПеИЧдЄ≠жЬАйХњзЪДйАТеЗПе≠РеЇПеИЧзЪДйХњеЇ¶MпЉМ дї•еПКиѓ•еЇПеИЧеПѓдї•еИТеИЖжИРињЩзІНе≠РеЇПеИЧзЪДдЄ™жХ∞N е¶ВеЇПеИЧпЉЪ 300 250 252 275 200 138 245 жКШеИЖжИРзЪДе≠РеЇПеИЧеИЖеИЂдЄЇ 300 275 200 138 ...
еЄЄзФ®еЫЊеГПжµЛиѓХеЇПеИЧ:foreman.cif(9-10) еЫ†еОЯеЃМжХіеЇПеИЧ姙姲,жЙАдї•еИЖжЦ≠дЄКдЉ†. еЫ†жµЛиѓХжЧґеЄЄеП™зФ®еЕґдЄ≠жЯРдЄАжЃµ,жХЕеП™дЄЛиљљдЄЙдЄ™жЦЗдїґдєЛдЄАе∞±еПѓ,еѓєжАІиГљжµЛиѓХж≤°жЬЙељ±еУН. е¶ВжЮЬйЬАи¶БзФ®еЃМжХіеЇПеИЧ,йЬАзФ®иљѓдїґе∞ЖеЇПеИЧињЮжО•иµЈжЭ•. <br>ињШжЬЙ...
дЄКиѓЊзФ®зЪДиѓЊжЬђиМГеЙСйЭТзЉЦеЖЩзЪДйЭЮзЇњжАІжЧґйЧіеЇПеИЧ еЕ®дє¶пЉМзФ®иµЈжЭ•ињШжШѓеЊИдЄНйФЩзЪДпЉМйЬАи¶БдЄКиѓЊзЪДеРМе≠¶еПѓдї•дљњзФ®
иІЖйҐСиљђеЫЊзЙЗеЇПеИЧз®ЛеЇПжШѓдЄАзІНеЈ•еЕЈпЉМеЃГиГље§Яе∞ЖиІЖйҐСжЦЗдїґжЛЖеИЖжИРдЄАз≥їеИЧињЮзї≠зЪДйЭЩжАБеЫЊеГПпЉМињЩдЇЫеЫЊеГПйАЪ媪襀зІ∞дЄЇеЄІгАВињЩзІНиљђжНҐеЬ®е§ЪзІНйҐЖеЯЯдЄ≠йГљжЬЙеЇФзФ®пЉМжѓФе¶Вељ±иІЖеРОжЬЯеИґдљЬгАБеК®зФїеИЫдљЬгАБзІСе≠¶з†Фз©ґжИЦиАЕзЃАеНХзЪДиІЖйҐСзЙЗжЃµжКУеПЦгАВдЄЛйЭҐе∞Жиѓ¶зїЖдїЛзїН...
SWFиљђPNGеЇПеИЧеЫЊеЈ•еЕЈжШѓдЄАзІНдЄУйЧ®зФ®дЇОе∞ЖAdobe FlashпЉИSWFпЉЙжЦЗдїґиљђжНҐдЄЇPNGеЫЊеГПеЇПеИЧзЪДиљѓдїґжИЦжЬНеК°гАВињЩзІНеЈ•еЕЈзЪДзЫЃзЪДжШѓдЄЇдЇЖжЦєдЊње§ДзРЖSWFжЦЗдїґдЄ≠зЪДеК®зФїеЖЕеЃєпЉМе∞§еЕґжШѓеЬ®SWFдЄНжФѓжМБжИЦиАЕжЧ†ж≥ХзЫіжО•еѓЉеЗЇдЄЇеЕґдїЦж†ЉеЉПжЧґгАВSWFжЦЗдїґйАЪеЄЄжШѓ...
йАЪињЗеЈЃеИЖињРзЃЧпЉМжИСдїђеПѓдї•е∞ЖжЧґйЧіеЇПеИЧиљђжНҐдЄЇеє≥з®≥жЧґйЧіеЇПеИЧпЉМзДґеРОеПѓдї•дљњзФ®зЩљеЩ™е£∞ж£Ай™МжЭ•з°ЃеЃЪжШѓеР¶е≠ШеЬ®йЪПжЬЇиѓѓеЈЃгАВ йАЪињЗдї•дЄКж≠•й™§пЉМжИСдїђеПѓдї•еїЇзЂЛдЄАдЄ™еРИйАВзЪД ARIMA ж®°еЮЛпЉМеєґеѓєеЕґињЫи°Мж£Ай™МпЉМдї•з°ЃеЃЪеЕґжШѓеР¶иГље§ЯжЬЙжХИеЬ∞йҐДжµЛжЬ™жЭ•еАЉгАВ ...
еЄЄзФ®еЫЊеГПжµЛиѓХеЇПеИЧ:foreman.cif(1-4) еЫ†еОЯеЃМжХіеЇПеИЧ姙姲,жЙАдї•еИЖжЦ≠дЄКдЉ†. еЫ†жµЛиѓХжЧґеЄЄеП™зФ®еЕґдЄ≠жЯРдЄАжЃµ,жХЕеѓєжµЛиѓХж≤°жЬЙељ±еУН. е¶ВжЮЬйЬАи¶БзФ®еЃМжХіеЇПеИЧ,еП™йЬАзФ®иљѓдїґе∞ЖеЇПеИЧињЮжО•иµЈжЭ•еН≥еПѓ. <br>
"йБЧдЉ†зЃЧж≥ХдЉШеМЦзЉЦз†БеЇПеИЧпЉЪеЃЮзО∞иґЕи°®йЭҐRCSзЉ©еЗПзЪДMATLABдЄОPythonеПМдї£з†БиІ£еЖ≥жЦєж°И",еЯЇдЇОйБЧдЉ†зЃЧж≥ХзЪДзЉЦз†БеЇПеИЧдЉШеМЦжКАжЬѓпЉЪеЃЮзО∞иґЕи°®йЭҐRCSзЉ©еЗПдЄОжЬАдљ≥жЉЂеПНе∞ДжХИжЮЬзЪДењЂйАЯиЃ°зЃЧ,йБЧдЉ†зЃЧж≥ХдЉШеМЦзЉЦз†БеЇПеИЧпЉМеЃЮзО∞зЉЦз†БиґЕи°®йЭҐrcsзЉ©еЗПгАВ...
ZEMAXжПРдЊЫдЄ§зІНдЄїи¶БзЪДиЃЊиЃ°ж®°еЉПпЉЪеЇПеИЧж®°еЉПпЉИSequential ModeпЉЙеТМйЭЮеЇПеИЧж®°еЉПпЉИNon-Sequential ModeпЉЙгАВеЇПеИЧж®°еЉПдЄїи¶БзФ®дЇОиЃЊиЃ°дЉ†зїЯзЪДйАПйХЬз≥їзїЯпЉМиАМйЭЮеЇПеИЧж®°еЉПеИЩйАВзФ®дЇОжЫіе§НжЭВзЪДиЗ™зԱ嚥жАБеЕЙе≠¶еЕГдїґжИЦйЭЮдЉ†зїЯеЗ†дљХ嚥зКґзЪДеЕЙе≠¶з≥їзїЯ...
йАЪињЗе∞ЖжЧґйЧіеЇПеИЧиљђжНҐдЄЇеЫЊеГПпЉМжИСдїђиГље§ЯеИ©зФ®дЄ∞еѓМзЪДиЃ°зЃЧжЬЇиІЖиІЙжКАжЬѓжЭ•жΥ糥е§НжЭВзЪДжЧґйЧіеЇПеИЧжХ∞жНЃпЉМињЩдЄНдїЕеҐЮеК†дЇЖж®°еЮЛзЪДиІ£йЗКжАІпЉМињШеПѓиГљжПРйЂШйҐДжµЛжАІиГљгАВзДґиАМпЉМињЩзІНжЦєж≥ХдєЯжЬЙеЕґжМСжИШпЉМжѓФе¶Ве¶ВдљХйАЙжЛ©еРИйАВзЪДеЫЊеГПи°®з§ЇжЦєж≥ХгАБе¶ВдљХе§ДзРЖйХњ...
3. иІЖйҐСиљђеЫЊзЙЗеЇПеИЧзЪДеЈ•еЕЈдЄОеСљдї§и°МеЈ•еЕЈ - GUIеЈ•еЕЈпЉЪе¶ВFFmpegгАБVirtualDubз≠ЙжПРдЊЫзФ®жИЈеПЛе•љзЪДзХМйЭҐпЉМеПѓиљїжЭЊе∞ЖиІЖйҐСеѓЉеЗЇдЄЇеЫЊзЙЗеЇПеИЧгАВдї•FFmpegдЄЇдЊЛпЉМеП™йЬАиЊУеЕ•з±їдЉЉ`ffmpeg -i input.avi output_%03d.png`зЪДеСљдї§пЉМе∞±иГље∞ЖиЊУеЕ•...
еЬ®еЃЮй™МдЄ≠пЉМйАЪињЗеѓєзФЯжИРзЪДmеЇПеИЧињЫи°МзЙєеЃЪзЪДињРзЃЧпЉМжИСдїђеПѓдї•еЊЧеИ∞KasamiеЇПеИЧзЪДе∞ПйЫЖпЉМињЩжЬЙеК©дЇОзРЖиІ£KasamiеЇПеИЧзЪДзФЯжИРжЬЇеИґеТМеЇФзФ®гАВ жЬАеРОпЉМжИСдїђи¶БжПРеИ∞зЪДжШѓGoldеЇПеИЧгАВGoldеЇПеИЧжШѓзФ±дЄ§дЄ™дЄНеРМmеЇПеИЧйАЪињЗеЉВжИЦжУНдљЬеЊЧеИ∞зЪДпЉМеЃГзїУеРИдЇЖдЄ§...
иѓ¶иІБ* еЕ≥дЇОеЇПеИЧеЯЇжЬђжУНдљЬ* еЕ≥дЇОеЕГзі†иµЛеАЉгАБеИ†йЩ§еЕГзі†гАБеИЗзЙЗиµЛеАЉ[PythonеЇПеИЧпЉЪеИЧи°®]
й¶ЦеЕИпЉМжИСдїђйЬАи¶БзРЖиІ£еЫЊзЙЗеЇПеИЧдЄОиІЖйҐСзЪДеЕ≥з≥їгАВиІЖйҐСжЬђиі®дЄКжШѓзФ±ињЮзї≠зЪДйЭЩжАБеЫЊеГПпЉИеЄІпЉЙењЂйАЯжТ≠жԌ嚥жИРзЪДпЉМињЩдЇЫеЄІеРИеЬ®дЄАиµЈе∞±жЮДжИРдЇЖеК®жАБзЪДзФїйЭҐгАВеЫ†ж≠§пЉМе∞ЖеЫЊзЙЗеЇПеИЧиљђжНҐдЄЇиІЖйҐСзЪДињЗз®Ле∞±жШѓе∞ЖињЩдЇЫеНХзЛђзЪДеЫЊзЙЗжМЙзЕІжЧґйЧій°ЇеЇПзїДеРИеєґиЃЊзљЃ...
ж†єжНЃеЇПеИЧзЪДйХњеЇ¶пЉМеПѓдї•е∞ЖеЕґеИЖдЄЇзЯ≠PNеЇПеИЧпЉИе¶ВmеЇПеИЧпЉЙеТМйХњPNеЇПеИЧпЉИе¶ВGoldеЇПеИЧгАБM sequenceгАБWalshеЇПеИЧз≠ЙпЉЙгАВ **PNеЇПеИЧзФЯжИРжЦєж≥Х** 1. **зЇњжАІеПНй¶ИзІїдљНеѓДе≠ШеЩ®пЉИLFSRпЉЙ**пЉЪжЬАеЄЄзФ®зЪДPNеЇПеИЧзФЯжИРжЦєж≥ХпЉМйАЪињЗдЄАдЄ™зЇњжАІеПНй¶ИеЗљжХ∞...
JsonToolsжШѓдЄАдЄ™дЄНйФЩзЪДJSONеЇПеИЧеМЦеТМеПНеЇПеИЧеМЦеКЯиГљеМЕ
гАКжЧґйЧіеЇПеИЧеИЖжЮРеПКеЇФзФ®:Rиѓ≠и®А еОЯдє¶зђђ2зЙИ гАЛдї•жШУдЇОзРЖиІ£зЪДжЦєеЉПиЃ≤ињ∞дЇЖжЧґйЧіеЇПеИЧж®°еЮЛеПКеЕґеЇФзФ® дЄїи¶БеЖЕеЃєеМЕжЛђпЉЪиґЛеКњ еє≥з®≥жЧґйЧіеЇПеИЧж®°еЮЛ йЭЮеє≥з®≥жЧґйЧіеЇПеИЧж®°еЮЛ ж®°еЮЛиѓЖеИЂ еПВжХ∞дЉ∞иЃ° ж®°еЮЛиѓКжЦ≠ йҐДжµЛ е≠£иКВж®°еЮЛ жЧґйЧіеЇПеИЧеЫЮељТж®°еЮЛ еЉВ...
"иІЖйҐСжЦЗдїґиљђеЫЊеГПеЇПеИЧ"зЪДеЈ•еЕЈдЄїи¶БеКЯиГљжШѓиѓїеПЦMP4жИЦAVIз≠ЙиІЖйҐСж†ЉеЉПпЉМеєґе∞ЖеЕґжѓПдЄАеЄІжПРеПЦеЗЇжЭ•пЉМдњЭе≠ШдЄЇзЛђзЂЛзЪДеЫЊеГПжЦЗдїґпЉМе¶Вjpgж†ЉеЉПгАВMP4жШѓдЄАзІНйЂШжХИзЪДеОЛзЉ©иІЖйҐСж†ЉеЉПпЉМеєњж≥ЫеЇФзФ®дЇОзљСзїЬжµБе™ТдљУеТМе≠ШеВ®пЉМиАМAVIеИЩжШѓдЄАзІНиЊГиАБдљЖжФѓжМБе§Ъ...