`
s103y
  • 浏览: 116722 次
  • 性别: Icon_minigender_1
  • 来自: 杭州
社区版块
存档分类
最新评论

排序算法

    博客分类：
  • java
算法J#Excel数据结构performance 
阅读更多
十四、排序（Sort）

这可能是最有趣的一节。排序的考题，在各大公司的笔试里最喜欢出了，但我看多数考得都很简单，通常懂得冒泡排序就差不多了，确实，我在刚学数据机构时候，觉得冒泡排序真的很“精妙”，我怎么就想不出呢？呵呵，其实冒泡通常是效率最差的排序算法，差多少？请看本文，你一定不会后悔的。

1、冒泡排序（Bubbler Sort）

前面刚说了冒泡排序的坏话，但冒泡排序也有其优点，那就是好理解，稳定，再就是空间复杂度低，不需要额外开辟数组元素的临时保存控件，当然了，编写起来也容易。

其算法很简单，就是比较数组相邻的两个值，把大的像泡泡一样“冒”到数组后面去，一共要执行N的平方除以2这么多次的比较和交换的操作（N为数组元素），其复杂度为Ο(n²)，如图：

 

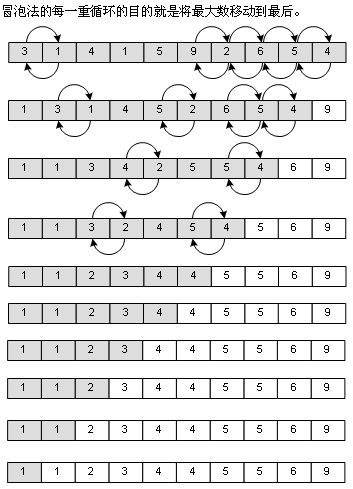
 2、直接插入排序（Straight Insertion Sort）

冒泡法对于已经排好序的部分（上图中，数组显示为白色底色的部分）是不再访问的，插入排序却要，因为它的方法就是从未排序的部分中取出一个元素，插入到已经排好序的部分去，插入的位置我是从后往前找的，这样可以使得如果数组本身是有序（顺序）的话，速度会非常之快，不过反过来，数组本身是逆序的话，速度也就非常之慢了，如图：

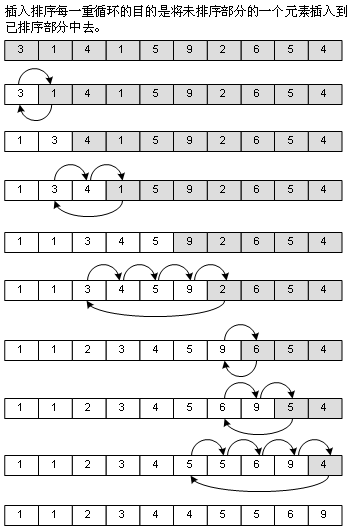
3、二分插入排序（Binary Insertion Sort）

这是对直接插入排序的改进，由于已排好序的部分是有序的，所以我们就能使用二分查找法确定我们的插入位置，而不是一个个找，除了这点，它跟插入排序没什么区别，至于二分查找法见我前面的文章（本系列文章的第四篇）。图跟上图没什么差别，差别在于插入位置的确定而已，性能却能因此得到不少改善。（性能分析后面会提到）

4、直接选择排序（Straight Selection Sort）

这是我在学数据结构前，自己能够想得出来的排序法，思路很简单，用打擂台的方式，找出最大的一个元素，和末尾的元素交换，然后再从头开始，查找第1个到第N-1个元素中最大的一个，和第N-1个元素交换……其实差不多就是冒泡法的思想，但整个过程中需要移动的元素比冒泡法要少，因此性能是比冒泡法优秀的。看图：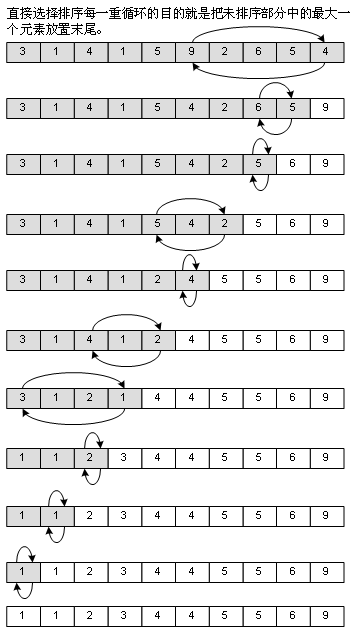

5、快速排序（Quick Sort）

快速排序是非常优秀的排序算法，初学者可能觉得有点难理解，其实它是一种“分而治之”的思想，把大的拆分为小的，小的再拆分为更小的，所以你一会儿从代码中就能很清楚地看到，用了递归。如图：

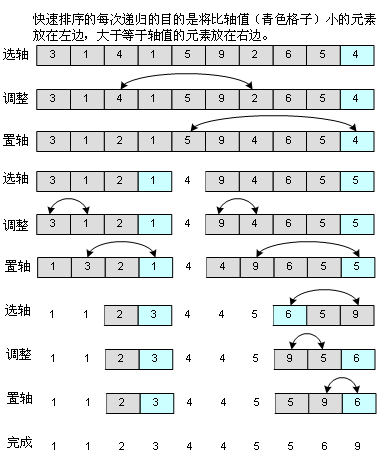
其中要选择一个轴值，这个轴值在理想的情况下就是中轴，中轴起的作用就是让其左边的元素比它小，它右边的元素不小于它。（我用了“不小于”而不是“大于”是考虑到元素数值会有重复的情况，在代码中也能看出来，如果把“>=”运算符换成“>”，将会出问题）当然，如果中轴选得不好，选了个最大元素或者最小元素，那情况就比较糟糕，我选轴值的办法是取出第一个元素，中间的元素和最后一个元素，然后从这三个元素中选中间值，这已经可以应付绝大多数情况。

6、改进型快速排序（Improved Quick Sort）

快速排序的缺点是使用了递归，如果数据量很大，大量的递归调用会不会导致性能下降呢？我想应该会的，所以我打算作这么种优化，考虑到数据量很小的情况下，直接选择排序和快速排序的性能相差无几，那当递归到子数组元素数目小于30的时候，我就是用直接选择排序，这样会不会提高一点性能呢？我后面分析。排序过程可以参考前面两个图，我就不另外画了。

7、桶排序（Bucket Sort）

这是迄今为止最快的一种排序法，其时间复杂度仅为Ο(n)，也就是线性复杂度！不可思议吧？但它是有条件的。举个例子：一年的全国高考考生人数为500万，分数使用标准分，最低100，最高900，没有小数，你把这500万元素的数组排个序。我们抓住了这么个非常特殊的条件，就能在毫秒级内完成这500万的排序，那就是：最低100，最高900，没有小数，那一共可出现的分数可能有多少种呢？一共有900-100+1=801，那么多种，想想看，有没有什么“投机取巧”的办法？方法就是创建801个“桶”，从头到尾遍历一次数组，对不同的分数给不同的“桶”加料，比如有个考生考了500分，那么就给500分的那个桶（下标为500-100）加1，完成后遍历一下这个桶数组，按照桶值，填充原数组，100分的有1000人，于是从0填到999，都填1000，101分的有1200人，于是从1000到2019，都填入101……如图：

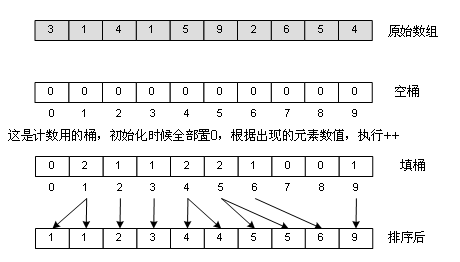
很显然，如果分数不是从100到900的整数，而是从0到2亿，那就要分配2亿个桶了，这是不可能的，所以桶排序有其局限性，适合元素值集合并不大的情况。

8、基数排序（Radix Sort）

基数排序是对桶排序的一种改进，这种改进是让“桶排序”适合于更大的元素值集合的情况，而不是提高性能。它的思想是这样的，比如数值的集合是8位整数，我们很难创建一亿个桶，于是我们先对这些数的个位进行类似桶排序的排序（下文且称作“类桶排序”吧），然后再对这些数的十位进行类桶排序，再就是百位……一共做8次，当然，我说的是思路，实际上我们通常并不这么干，因为C++的位移运算速度是比较快，所以我们通常以“字节”为单位进行桶排序。但下图为了画图方便，我是以半字节（4 bit）为单位进行类桶排序的，因为字节为单位进行桶排得画256个桶，有点难画，如图：

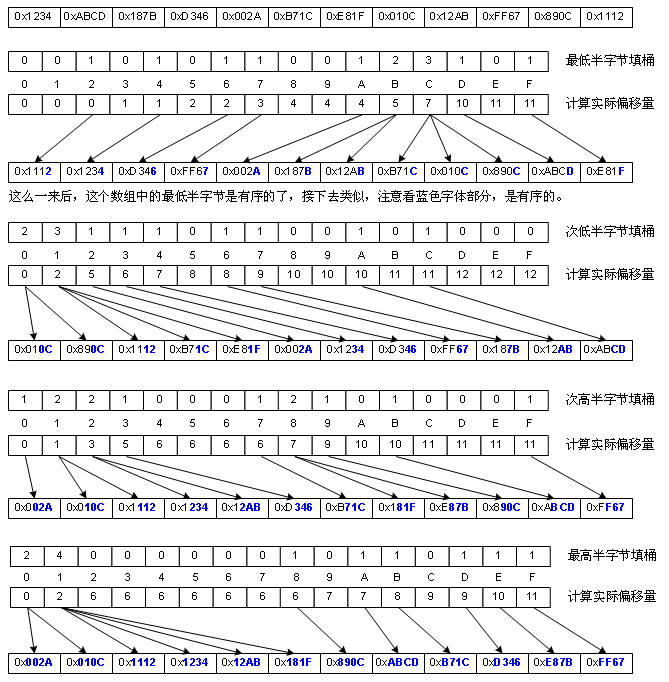
基数排序适合数值分布较广的情况，但由于需要额外分配一个跟原始数组一样大的暂存空间，它的处理也是有局限性的，对于元素数量巨大的原始数组而言，空间开销较大。性能上由于要多次“类桶排序”，所以不如桶排序。但它的复杂度跟桶排序一样，也是Ο(n)，虽然它用了多次循环，但却没有循环嵌套。

9、性能分析和总结

先不分析复杂度为Ο(n)的算法，因为速度太快，而且有些条件限制，我们先分析前六种算法，即：冒泡，直接插入，二分插入，直接选择，快速排序和改进型快速排序。

我的分析过程并不复杂，尝试产生一个随机数数组，数值范围是0到7FFF，这正好可以用C++的随机函数rand()产生随机数来填充数组，然后尝试不同长度的数组，同一种长度的数组尝试10次，以此得出平均值，避免过多波动，最后用Excel对结果进行分析，OK，上图了。

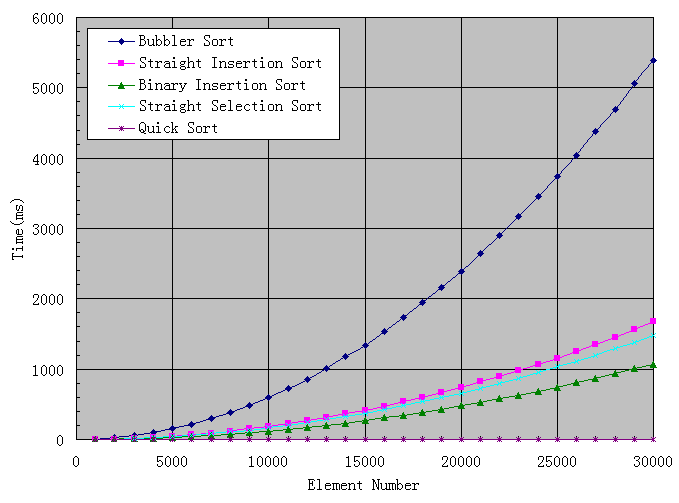
最差的一眼就看出来了，是冒泡，直接插入和直接选择旗鼓相当，但我更偏向于使用直接选择，因为思路简单，需要移动的元素相对较少，况且速度还稍微快一点呢，从图中看，二分插入的速度比直接插入有了较大的提升，但代码稍微长了一点点。

令人感到比较意外的是快速排序，3万点以内的快速排序所消耗的时间几乎可以忽略不计，速度之快，令人振奋，而改进型快速排序的线跟快速排序重合，因此不画出来。看来要对快速排序进行单独分析，我加大了数组元素的数目，从5万到150万，画出下图：

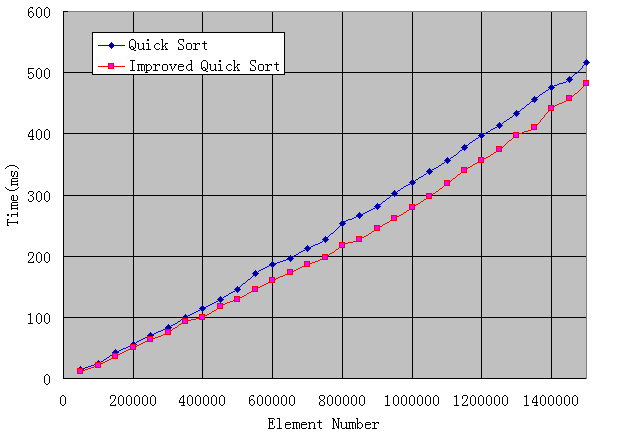
可以看到，即便到了150万点，两种快速排序也仅需差不多半秒钟就完成了，实在快，改进型快速排序性能确实有微略提高，但并不明显，从图中也能看出来，是不是我设置的最小快速排序元素数目不太合适？但我尝试了好几个值都相差无几。

最后看线性复杂度的排序，速度非常惊人，我从40万测试到1200万，结果如图：

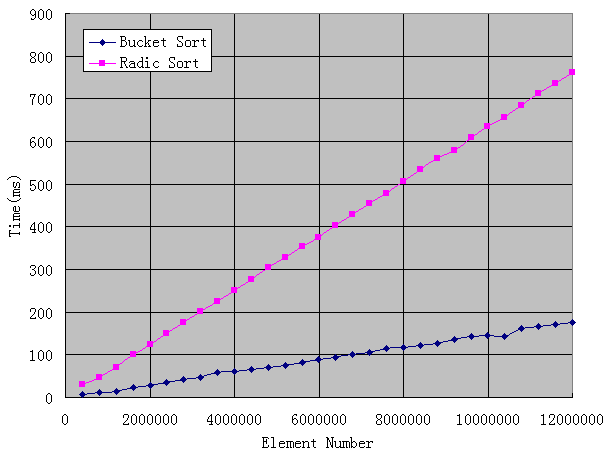
可见稍微调整下算法，速度可以得到质的飞升，而不是我们以前所认为的那样：再快也不会比冒泡法快多少啊？

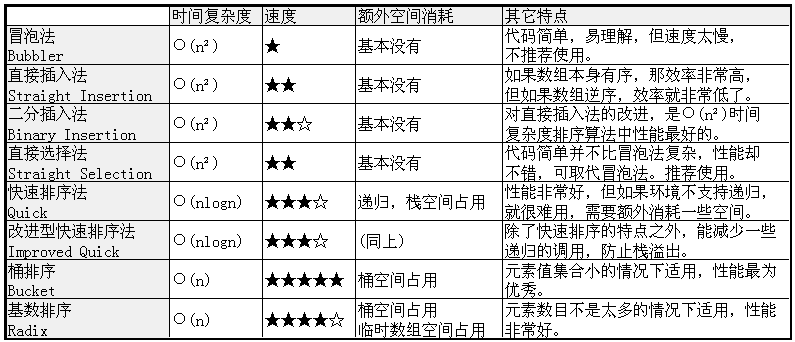
我最后制作一张表，比较一下这些排序法：

还有一个最后：附上我的代码。

#include "stdio.h"
#include "stdlib.h"
#include "time.h"
#include "string.h"

void BubblerSort(int *pArray, int iElementNum);
void StraightInsertionSort(int *pArray, int iElementNum);
void BinaryInsertionSort(int *pArray, int iElementNum);
void StraightSelectionSort(int *pArray, int iElementNum);
void QuickSort(int *pArray, int iElementNum);
void ImprovedQuickSort(int *pArray, int iElementNum);
void BucketSort(int *pArray, int iElementNum);
void RadixSort(int *pArray, int iElementNum);

//Tool functions.
void PrintArray(int *pArray, int iElementNum);
void StuffArray(int *pArray, int iElementNum);

inline void Swap(int& a, int& b);

#define SINGLE_TEST

int main(int argc, char* argv[])
{
    srand(time(NULL));
#ifndef SINGLE_TEST
    int i, j, iTenTimesAvg;
    for(i=50000; i<=1500000; i+=50000)
    {
        iTenTimesAvg = 0;
        for(j=0; j<10; j++)
        {
            int iElementNum = i;
            int *pArr = new int[iElementNum];
            StuffArray(pArr, iElementNum);
            //PrintArray(pArr, iElementNum);
            clock_t ctBegin = clock();
            ImprovedQuickSort(pArr, iElementNum);
            //PrintArray(pArr, iElementNum);
            clock_t ctEnd = clock();
            delete[] pArr;

            iTenTimesAvg += ctEnd-ctBegin;
        }
        printf("%d\t%d\n", i, iTenTimesAvg/10);
    }
#else
    //Single test
    int iElementNum = 100;
    int *pArr = new int[iElementNum];
    StuffArray(pArr, iElementNum);
    PrintArray(pArr, iElementNum);
    clock_t ctBegin = clock();
    QuickSort(pArr, iElementNum);
    clock_t ctEnd = clock();
    PrintArray(pArr, iElementNum);
    delete[] pArr;
    int iTenTimesAvg = ctEnd-ctBegin;
    printf("%d\t%d\n", iElementNum, iTenTimesAvg);
#endif
    return 0;
}

void BubblerSort(int *pArray, int iElementNum)
{
    int i, j, x;
    for(i=0; i<iElementNum-1; i++)
    {
        for(j=0; j<iElementNum-1-i; j++)
        {
            if(pArray[j]>pArray[j+1])
            {
                //Frequent swap calling may lower performance.
                //Swap(pArray[j], pArray[j+1]);

                //Do you think bit operation is better? No! Please have a try.
                //pArray[j] ^= pArray[j+1];
                //pArray[j+1] ^= pArray[j];
                //pArray[j] ^= pArray[j+1];
                
                //This kind of traditional swap is the best.
                x = pArray[j];
                pArray[j] = pArray[j+1];
                pArray[j+1] = x;
            }
        }
    }
}

void StraightInsertionSort(int *pArray, int iElementNum)
{
    int i, j, k;
    for(i=0; i<iElementNum; i++)
    {
        int iHandling = pArray[i];
        for(j=i; j>0; j--)
        {
            if(iHandling>=pArray[j-1])
                break;
        }

        for(k=i; k>j; k--)
            pArray[k] = pArray[k-1];
        pArray[j] = iHandling;
    }
}

void BinaryInsertionSort(int *pArray, int iElementNum)
{
    int i, j, k;
    for(i=0; i<iElementNum; i++)
    {
        int iHandling = pArray[i];
        
        int iLeft = 0;
        int iRight = i-1;
        while(iLeft<=iRight)
        {
            int iMiddle = (iLeft+iRight)/2;
            if(iHandling < pArray[iMiddle])
            {
                iRight = iMiddle-1;
            }
            else if(iHandling > pArray[iMiddle])
            {
                iLeft = iMiddle+1;
            }
            else
            {
                j = iMiddle + 1;
                break;
            }
        }

        if(iLeft>iRight)
            j = iLeft;
        
        for(k=i; k>j; k--)
            pArray[k] = pArray[k-1];
        pArray[j] = iHandling;
    }
}

void StraightSelectionSort(int *pArray, int iElementNum)
{
    int iEndIndex, i, iMaxIndex, x;

    for(iEndIndex=iElementNum-1; iEndIndex>0; iEndIndex--)
    {
        for(i=0, iMaxIndex=0; i<iEndIndex; i++)
        {
            if(pArray[i]>=pArray[iMaxIndex])
                iMaxIndex = i;
        }
        x = pArray[iMaxIndex];
        pArray[iMaxIndex] = pArray[iEndIndex];
        pArray[iEndIndex] = x;
    }    
}

void BucketSort(int *pArray, int iElementNum)
{
    //This is really buckets.
    int buckets[RAND_MAX];
    memset(buckets, 0, sizeof(buckets));
    int i;
    for(i=0; i<iElementNum; i++)
    {
        ++buckets[pArray[i]-1];
    }

    int iAdded = 0;
    for(i=0; i<RAND_MAX; i++)
    {
        while((buckets[i]--)>0)
        {
            pArray[iAdded++] = i;
        }
    }
}

void RadixSort(int *pArray, int iElementNum)
{
    int *pTmpArray = new int[iElementNum];

    int buckets[0x100];
    memset(buckets, 0, sizeof(buckets));
    int i;
    for(i=0; i<iElementNum; i++)
    {
        ++buckets[(pArray[i])&0xFF];
    }
    
    //Convert number to offset
    int iPrevNum = buckets[0];
    buckets[0] = 0;
    int iThisNum;
    for(i=1; i<0x100; i++)
    {
        iThisNum = buckets[i];
        buckets[i] = buckets[i-1] + iPrevNum;
        iPrevNum = iThisNum;
    }

    for(i=0; i<iElementNum; i++)
    {
        pTmpArray[buckets[(pArray[i])&0xFF]++] = pArray[i];
    }

    //////////////////////////////////////////////////////////////////////////
    memset(buckets, 0, sizeof(buckets));
    for(i=0; i<iElementNum; i++)
    {
        ++buckets[(pTmpArray[i]>>8)&0xFF];
    }

    //Convert number to offset
    iPrevNum = buckets[0];
    buckets[0] = 0;
    iThisNum;
    for(i=1; i<0x100; i++)
    {
        iThisNum = buckets[i];
        buckets[i] = buckets[i-1] + iPrevNum;
        iPrevNum = iThisNum;
    }

    for(i=0; i<iElementNum; i++)
    {
        pArray[buckets[((pTmpArray[i]>>8)&0xFF)]++] = pTmpArray[i];
    }

    delete[] pTmpArray;
}

void QuickSort(int *pArray, int iElementNum)
{
    int iTmp;

    //Select the pivot make it to the right side.
    int& iLeftIdx = pArray[0];
    int& iRightIdx = pArray[iElementNum-1];
    int& iMiddleIdx = pArray[(iElementNum-1)/2];
    if(iLeftIdx>iMiddleIdx)
    {
        iTmp = iLeftIdx;
        iLeftIdx = iMiddleIdx;
        iMiddleIdx = iTmp;
    }
    if(iRightIdx>iMiddleIdx)
    {
        iTmp = iRightIdx;
        iRightIdx = iMiddleIdx;
        iMiddleIdx = iTmp;
    }
    if(iLeftIdx>iRightIdx)
    {
        iTmp = iLeftIdx;
        iLeftIdx = iRightIdx;
        iRightIdx = iTmp;
    }

    //Make pivot's left element and right element.
    int iLeft = 0;
    int iRight = iElementNum-2;
    int& iPivot = pArray[iElementNum-1];
    while (1)
    {
        while (iLeft<iRight && pArray[iLeft]<iPivot) ++iLeft;
        while (iLeft<iRight && pArray[iRight]>=iPivot) --iRight;
        if(iLeft>=iRight)
            break;
        iTmp = pArray[iLeft];
        pArray[iLeft] = pArray[iRight];
        pArray[iRight] = iTmp;
    }

    //Make the i
    if(pArray[iLeft]>iPivot)
    {
        iTmp = pArray[iLeft];
        pArray[iLeft] = iPivot;
        iPivot = iTmp;
    }

    if(iLeft>1)
        QuickSort(pArray, iLeft);

    if(iElementNum-iLeft-1>=1)
        QuickSort(&pArray[iLeft+1], iElementNum-iLeft-1);

}

void ImprovedQuickSort(int *pArray, int iElementNum)
{
    int iTmp;
    
    //Select the pivot make it to the right side.
    int& iLeftIdx = pArray[0];
    int& iRightIdx = pArray[iElementNum-1];
    int& iMiddleIdx = pArray[(iElementNum-1)/2];
    if(iLeftIdx>iMiddleIdx)
    {
        iTmp = iLeftIdx;
        iLeftIdx = iMiddleIdx;
        iMiddleIdx = iTmp;
    }
    if(iRightIdx>iMiddleIdx)
    {
        iTmp = iRightIdx;
        iRightIdx = iMiddleIdx;
        iMiddleIdx = iTmp;
    }
    if(iLeftIdx>iRightIdx)
    {
        iTmp = iLeftIdx;
        iLeftIdx = iRightIdx;
        iRightIdx = iTmp;
    }
    
    //Make pivot's left element and right element.
    int iLeft = 0;
    int iRight = iElementNum-2;
    int& iPivot = pArray[iElementNum-1];
    while (1)
    {
        while (iLeft<iRight && pArray[iLeft]<iPivot) ++iLeft;
        while (iLeft<iRight && pArray[iRight]>=iPivot) --iRight;
        if(iLeft>=iRight)
            break;
        iTmp = pArray[iLeft];
        pArray[iLeft] = pArray[iRight];
        pArray[iRight] = iTmp;
    }
    
    //Make the i
    if(pArray[iLeft]>iPivot)
    {
        iTmp = pArray[iLeft];
        pArray[iLeft] = iPivot;
        iPivot = iTmp;
    }
    
    if(iLeft>30)
        ImprovedQuickSort(pArray, iLeft);
    else
        StraightSelectionSort(pArray, iLeft);
    
    if(iElementNum-iLeft-1>=30)
        ImprovedQuickSort(&pArray[iLeft+1], iElementNum-iLeft-1);
    else
        StraightSelectionSort(&pArray[iLeft+1], iElementNum-iLeft-1);
}

void StuffArray(int *pArray, int iElementNum)
{
    int i;
    for(i=0; i<iElementNum; i++)
    {
        pArray[i] = rand();
  
分享到：
| Hibernate缓存机制
评论
发表评论

您还没有登录,请您登录后再发表评论

相关推荐

Magicbox
Global site tag (gtag.js) - Google Analytics