NUC: http://acm.nuc.edu.cn/OJ/problem.php?pid=1396
Description:
The Head Elder of the tropical island of Lagrishan has a problem. A
burst of foreign aid money was spent on extra roads between villages
some years ago. But the jungle overtakes roads relentlessly, so the
large road network is too expensive to maintain. The Council of Elders
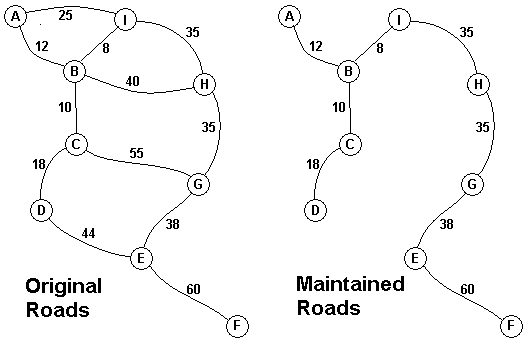
must choose to stop maintaining some roads. The map above on the left
shows all the roads in use now and the cost in aacms per month to
maintain them. Of course there needs to be some way to get between all
the villages on maintained roads, even if the route is not as short as
before. The Chief Elder would like to tell the Council of Elders what
would be the smallest amount they could spend in aacms per month to
maintain roads that would connect all the villages. The villages are
labeled A through I in the maps above. The map on the right shows the
roads that could be maintained most cheaply, for 216 aacms per month.
Your task is to write a program that will solve such problems.
Input:
The input consists of one to 100 data sets, followed by a final line containing only
0. Each data set starts with a line containing only a number n
,
which is the number of villages, 1 < n
< 27, and the villages
are labeled with the first n
letters of the alphabet, capitalized.
Each data set is completed with n
-1 lines that start with village
labels in alphabetical order. There is no line for the last village.
Each line for a village starts with the village label followed by a number,
k
,
of roads from this village to villages with labels later
in the
alphabet. If k
is greater than 0, the line continues with
data for each of the k
roads. The data for each road is the
village label for the other end of the road followed by the monthly maintenance
cost in aacms for the road. Maintenance costs will be positive integers
less than 100. All data fields in the row are separated by single
blanks. The road network will always allow travel between all the
villages. The network will never have more than 75 roads. No
village will have more than 15 roads going to other villages (before or
after in the alphabet). In the sample input below, the
first data set goes with the map above.
Output:
The output is one integer per line for each data set: the minimum cost in aacms
per month to maintain a road system that connect all the villages. Caution
:
A brute force solution that examines every possible set of roads will not
finish within the one minute time limit.
Example Input:
9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0
Example Output:
216
30
题解:该题使用的算法是Kruskal最小生成树
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define E 27*27
#define N 27
typedef struct
{
int v1;
int v2; //节点v1,v2是两个节点的序号
int cost; //边的权值
} EdgeType;
EdgeType edges[E], T[N-1];
int Find(int father[], int v)
{
/*
*寻找顶点v所在树的根节点
*/
int t = v;
while(father[t] >= 0)
{
t = father[t];
}
return t;
}
void Kruskal(EdgeType edges[], EdgeType T[])
{
/*
*用Kruskal方法构造图的最小生成树
*edges是图中的各条边,而且已经按其权值从小到大排序,
*最小生成树的边在T中
*/
int i, j;
int father[N];
int vf1, vf2;
memset(father, -1, sizeof(father));
i = j = 0;
while(i < E && j < N-1)
{
vf1 = Find(father, edges[i].v1);
vf2 = Find(father, edges[i].v2);
if(vf1 != vf2)
{
/*vf1, vf2不在同一个集合中,联通两个集合*/
father[vf2] = vf1;
T[j] = edges[i];
j++;
}
i++;
}
}
int comp(const void *a, const void *b)
{
EdgeType p = *(EdgeType *)a;
EdgeType q = *(EdgeType *)b;
if((p.cost) >= (q.cost)) return 1;
else return -1;
}
int main()
{
int i, j, k;
int n, m;
int cost, total_cost;
char ch1, ch2;
while(scanf("%d", &n) && n)
{
getchar();
k = 0;
total_cost = 0;
/*
*输入节点以及边的权值
*/
for(i = 0; i < n-1; i++)
{
scanf("%c %d", &ch1, &m);
getchar();
for(j = 0; j < m; j++)
{
scanf("%c %d", &ch2, &cost);
getchar();
edges[k].v1 = ch1-'A'+1;
edges[k].v2 = ch2-'A'+1;
edges[k].cost = cost;
k++;
}
}
/*
*对节点按权值大小进行排序
*/
qsort(edges, k, sizeof(EdgeType), comp);
Kruskal(edges, T); //生成最小树
for(i = 0; i < n-1; i++)
{
/*计算总的最小权值*/
total_cost += T[i].cost;
}
printf("%d\n", total_cost);
}
return 0;
}
分享到:





相关推荐
Jungle Roads可能是指寻找最小生成树的问题,如Prim算法或Kruskal算法,用于找到连接所有顶点的边权重之和最小的子集。Stockbroker Grapevine则可能与网络流或最大匹配问题有关,模拟股票交易中的信息传递或资源分配...
本资源提供了多种关于最小生成树的题目,例如 Constructing Roads、畅通工程、Connect the Cities、Jungle Roads等。 并查集 并查集(Union-Find)是一种数据结构,用于处理不相交集的合并和查询操作。并查集广泛...
JungleRoads (丛林道路) - **问题描述**:可能涉及到在复杂地形中规划道路,需要考虑道路的成本和效率。 - **算法应用**:最小生成树算法如Prim或Kruskal,用于构建连接所有节点的最低成本路径。 #### 4. ...
笔者本人写的一些代码,供大家参考. 包括但不限于镜子迷宫、棋盘问题、最长上升子序列、jungle roads gone fishing、nested dolls、paid roads、red and black等等 绝大部分是数据结构与算法课的作业
12. **1406 - Jungle Roads**:丛林道路规划问题。 13. **1053 - FDNY to the Rescue!**:消防救援问题。 14. **1055 - Oh, Those Aching Feet!**:脚痛问题。 15. **1059 - What's In a Name**:名字相似度问题。 ...
11. **1251 Jungle Roads MST** - **知识点**: 图论中的最小生成树 - **解析**: 使用最小生成树(Minimum Spanning Tree, MST)算法来解决特定问题。最小生成树是指在一个加权无向图中,选取图中所有顶点的一个...
#### 1251 Jungle Roads - MST - **知识点**:最小生成树(MST),一种用于构造连接图中所有顶点且总权重最小的树的算法,如Prim算法或Kruskal算法。 #### 1273 Drainage Ditches - 最大流 - **知识点**:最大流...
- **1406 Jungle Roads**: 丛林道路问题,适合使用图论中的最短路径算法。 - **1053 FDNY to the Rescue!**: 救援问题,涉及图论中的最短路径算法。 - **1055 Oh, Those Aching Feet**: 脚痛问题,适合使用动态规划...
ZJU_Main 主页 下一页 ZJU 题型分类 文演整理版 2008-3-23 数论: 1007 Numerical Summation of a Series 简单题,还是蛮有意思的 1045 HangOver 简单题 ... 1049 I Think I Need a Houseboat 简单题 ...
ZJU 题型分类 ZJU_Main 主页 下一页 ZJU 题型分类 文演整理版 2008-3-23 数论: 1007 Numerical Summation of a Series 简单题,还是蛮有意思的 ... 1049 I Think I Need a Houseboat 简单题 ...